Теория параллельных прямых. Теория треугольника, страница 10

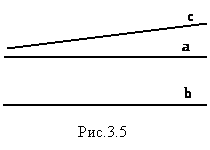
2) Прямые а и c не пересекаются с прямой b. Могут ли прямые а и с иметь общую точку(рис.3.5)? Они могут пересекаться, если через одну точку можно провести больше одной прямой, непересекающейся с данной. Но на рисунке видно, что, если прямая с пересечет прямую а, то она пересечет и прямую b, но прямые с и b не пересекаются.

С другой стороны нам известно, что не всегда истинно то, что мы видим.

Итак, сколько существует прямых, не пересекающихся с данной и проходящих через одну точку, не лежащую на данной прямой. Возможные ответы: ни одной, одна, две или больше двух.

Из истории математики известно, что этот вопрос вызывал интерес математиков в течение двух с половиной тысяч лет. Мы не имеем возможности вдаваться в содержание этой проблемы, но что же тогда делать? Давайте договоримся и примем одно из этих утверждений как аксиому.

Аксиома параллельности:

Через точку, не лежащую на данной прямой, можно провести не более одной прямой, не пересекающейся с данной.

Название этой аксиомы поясняет следующее определение.

Две прямые называются параллельными, если они не пересекаются и удовлетворяют условию аксиомы параллельности.

Специально подчеркнем, что после того, как мы приняли условие аксиомы параллельности, слова параллельные и непересекающиеся стали синонимами.

Отрезки (лучи), лежащие на параллельных прямых, также параллельны.

Параллельность прямых a и b принято обозначать так: a||b.

Теперь, когда мы договорились об аксиоме параллельности, мы можем определить еще одно понятие.

Поверхность, на которой выполняется аксиома параллельности называется плоскостью.

Сравните прямые на рисунках 3.6 и3.7.

На рис.3.6 прямые а и b не пересекаются, но если их продолжить, то прямые пересекутся. А если продолжить прямые на рис.3.7? Вы уверены, что они не пересекутся, например, через 100м, 100км?

Вопрос 1. Каким же образом можно проверить параллельность прямых? По рисунку это проверить невозможно. Но как узнать, параллельны прямые или нет?

Нужно сделать дополнительное построение, то есть привлечь ещё одну геометрическую фигуру. Возьмём в качестве такой дополнительной фигуры прямую.

3.2. Взаимное расположение трех прямых.

Как могут располагаться три прямые по отношению друг к другу? Изобразим разные случаи. Возможны четыре случая:

А) Прямая c пересекает обе пересекающиеся прямые a и b, каждую в своей точке.	Рис.3.8
Б) Прямые а и b параллельны. Прямая c пересекает прямую a. Пересекает ли прямая c прямую b? Видно, что c пересекает b.Значит, если прямая пересекает одну из параллельных прямых, то она пересекает и другую! Как это доказать? ( Вопрос 2 )	Рис.3.9
В) Прямая c пересекается с прямыми a и b в их общей точке.	Рис.3.10
Г) Прямые а и b параллельны. Прямая c параллельна прямой a. Параллельна ли прямая c прямой b? Видно, что c||b. Значит, если прямая параллельна одной из двух параллельных прямых, то она параллельна и другой! Это так, но как это доказать? (Вопрос 3)	Рис.3.11