Теперь, когда мы решили проблему определения треугольника, давайте подумаем, в каком отношении могут находиться элементы треугольника. Произвольны они или находятся в какой-то зависимости друг от друга?
Как вы знаете, если отложить любые две точки, их всегда можно соединить отрезком. Так же можно построить отрезок, задав любую длину. Но всегда ли мы сможем восстановить треугольник по произвольно заданным элементам? Мы уже выяснили, что вершины треугольника не могут лежать на одной прямой. А в каком отношении находятся углы и стороны треугольника? Рассмотрим этот вопрос подробно.
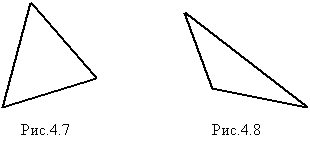
Произвольны ли величины углов в треугольнике? Рассмотрим все виды углов. На рисунке 4.7 мы можем видеть треугольник с тремя острыми углами. На рисунке 4.8 два угла острые, а третий – тупой.
А бывают ли треугольники, в которых два тупых угла? Попробуем изобразить.
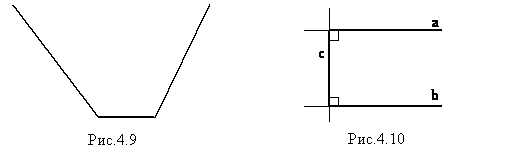
Построим один из тупых углов. Одна из сторон этого угла будет стороной второго тупого угла. Отложим его в той же полуплоскости, что и первый. На рисунке 4.9 видно, что стороны углов, не являющиеся общими, не пересекаются при любом их продолжении. Можно сделать предположение, что не бывает треугольников с двумя тупыми углами.
Существуют ли треугольники, в которых два прямых угла? Построим эти углы аналогично предыдущему случаю (рис.4.10). Заметим, что два прямых угла в сумме дают развернутый угол. Кроме того, эти углы являются внутренними односторонними при прямых a и b и их секущей c, полученных продолжением сторон углов. То есть прямые a и b параллельны, а значит, не существуют треугольники с двумя прямыми углами.
На основании аналогичного рассуждения можно сделать вывод, что не существуют треугольники, у которых сумма двух углов равна 180º. Восстановите это рассуждение самостоятельно.
Итак, можно сделать вывод, что сумма двух любых углов треугольника не может быть больше либо равняться 180º.
Как вы помните, треугольник мы получили, рассматривая общий случай взаимного расположения трех прямых, и всегда можем продлить стороны треугольника (рис.4.5, а).
Но этот вариант взаимного расположения трех прямых мы уже рассматривали вместе со случаем пересечения двух параллельных прямых секущей. Тогда мы выяснили:
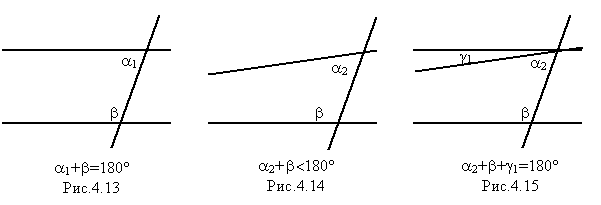
¨ если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 180° (рис.4.13).
¨ если пересекающиеся прямые пересечены секущей, то сумма внутренних односторонних углов не равна 180° и меньше с той стороны, с которой прямые пересекаются (рис.4.14).
Иными словами, когда прямые не пересекались, сумма внутренних односторонних углов была равна 180°. А когда пересеклись, она уменьшилась. Но на сколько? Чтобы узнать это, объединим два эти два варианта (рис.4.15).
На рисунке 4.15 видно, что сумма уменьшилась на угол γ1.
А что же там, где прямые пересекаются? Расширим границы рисунка так, чтобы было видно точку пересечения. Обозначим вершины треугольника, образованного пересекающимися прямыми буквами А, В, С.
 Рис.4.16
Рис.4.16
На рисунке 4.16 видно, что третий угол треугольника γ и угол γ1 равны как внутренние накрест лежащие при параллельных прямых АВ и ЕС и секущей АС. Это означает, что сумма внутренних углов треугольника равна 180º.
Мы получили удивительный факт. Оказывается, сумма внутренних углов любых треугольников имеет постоянное значение!
Итак, мы доказали теорему о сумме внутренних углов треугольника.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.