Теория параллельных прямых. Теория треугольника, страница 21

Два треугольника называются равными, если для каждой стороны одного из них найдется равная ей сторона другого.

Это определение можно понять так, что из двух данных треугольников мы выбираем один – первый. И проверяем, для каждой ли его стороны есть равная ей сторона второго. Оказывается такое понимание неправильное. Приведем пример, когда оно не работает.

На рисунке 4.23 видно, что при выше упомянутом понимании определения равенства треугольников, равнобедренный треугольник равен неравнобедренному.

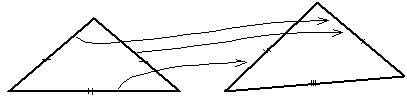
Рис.4.23

Мы видим, что для каждой стороны первого треугольника есть равная ей сторона второго. Но для третьей стороны второго нет равной стороны первого.

Эту трудность можно устранить, если понимать определение как двойное (то есть в обе стороны).

Но есть и другая трудность. В треугольнике кроме сторон есть еще и углы. При таком определении остается не ясным, будут ли равны углы. А, значит, в определение нужно включать их сравнение. Итак, сформулируем определение равенства треугольников.

Треугольники называются равными, если:

1. если для каждой стороны одного из них найдется равная ей сторона другого;

2. если для каждого угла одного из них найдется равный ему угол другого.

Напомним, что это определение нужно понимать как двойное (то есть в обе стороны).

4.4. Признаки равенства треугольников.

В определении равенства треугольников говорится: для того, чтобы установить, равенство треугольников, нужно сравнить шесть элементов первого и шесть элементов второго.

Но возможно будет достаточно и меньшего количества элементов? Рассмотрим этот вопрос подробнее.

Какие возможны варианты?

Достаточно ли равенства пяти элементов? Возможны две комбинации:

1. Три стороны одного треугольника равны трем сторонам другого и два угла одного треугольника равны двум углам другого;

2. Две стороны одного треугольника равны двум сторонам другого и три угла одного треугольника равны трем углам другого.

В первом случае, по теореме о сумме углов треугольника (которая говорит о том, что сумма углов одна и та же во всех треугольниках) третьи углы также будут равны. А это означает, что в этом случае треугольники равны по определению.

Приведем пример не равных треугольников, для которых выполняется условие пункта 2.

На рисунке 4.24 можем видеть два треугольника: АВС и КВМ. В этих треугольниках КВ=АС, КМ=ВС, то есть для двух сторон треугольника АВС есть равные им в треугольнике КВМ и наоборот. Кроме того, для каждого из трех углов треугольника АВС есть равные им в треугольнике КВМ и наоборот. Но мы видим, что эти треугольники не равны.

Итак, если мы знаем, что две стороны одного треугольника равны двум сторонам другого и три угла одного треугольника равны трем углам другого и ничего больше эти треугольники не знаем, то этого не достаточно, чтобы установить равенство двух треугольников. Тем более не достаточно будет меньшего количества углов и сторон.

Значит, осталось рассмотреть два варианта

1.  Три стороны одного треугольника равны трем сторонам другого треугольника и один из углов одного равен одному из углов другого.

2.  Три стороны одного треугольника равны трем сторонам другого треугольника.

На рисунке 4.25 мы видим два треугольника, у которых для каждой из сторон одного треугольника найдется равная ей сторона в другом треугольнике

Равны ли эти треугольники?

Каждая сторона любого треугольника является поперечиной противолежащего угла. Кроме того, в треугольниках на рисунке 4.25 равные стороны являются соответствующими поперечинами противолежащих им углов. Поэтому углы, противолежащие равным сторонам, равны.