Теория параллельных прямых. Теория треугольника, страница 17

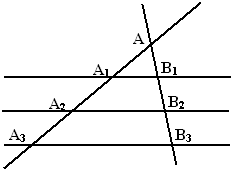
Рис.3.35

Задание 6. Сформулируйте теорему Фалеса для произвольного числа параллельных прямых.

Задание 7. Часто теорема Фалеса применяется для решения следующей задачи: разделите произвольный отрезок на n равных частей. Возьмите конкретное n и решите эту задачу.

Глава 4. Теория треугольников.

В третьей главе мы рассматривали взаимное расположение трех прямых. Вспомним типичные случаи:

Рис.4.1

Из этих четырех случаев три – 4.1, б, в, г случаи особого расположения прямых, то есть подчинены некоторым условиям. Не рассмотренным оказался первый – случай общего расположения. Эти три прямые делят плоскость на семь областей, одна из которых ограниченная, конечная. Изучим границу этой области подробнее.

4.1. Определение треугольника.

Рассмотрим рисунок 4.2. На нем можно последовательно выделить геометрические фигуры трех основных типов.

Вначале – три точки пересечения прямых (рис.4.3). Эти точки определяют три отрезка (рис.4.4), у которых концы совпадают с точками пересечения.

Эти отрезки образуют попарно три угла (рис.4.5, а). Таким образом, можно построить объект, состоящий из девяти элементов, по три элемента каждого из трех типов (рис.4.5, б).

Рис.4.5

С помощью генетического определения мы построили объект, изображенный на рисунке 4.5, б. Попробуем дать ему формально-логическое определение.

Геометрическая фигура, представляющая собой систему из трех точек, трех соединяющих их отрезков и трех образованных этими отрезками углов называется треугольником. Точки, входящие в состав этой фигуры, называются вершинами треугольника, отрезки, – сторонами треугольника, а углы, – внутренними углами треугольника.

Как перейти от рисунка треугольника (рис.4.5, б) к тексту про треугольник? Для этого треугольник обозначают указанием вершин. Слово "треугольник" иногда заменяют значком D. Таким образом, рисунку 4.5, в соответствует кусочек текста DABC.

Соответствует ли формальное определение треугольника объекту, изображенному на рисунке 4.5, б? Отметим три произвольные точки. Их всегда можно соединить попарно тремя отрезками. Но всегда ли мы получим треугольник?

Рис.4.6

Фигура, изображенная на рисунке 4.6, а – треугольник? И да, и нет. Да, потому что соответствует формальному определению треугольника. Нет, так как по внешнему виду – это отрезок. Более того, эту фигуру нельзя получить, пересекая три прямые. Такие фигуры будем называть вырожденными треугольниками и в дальнейшем будем использовать их для проверки утверждений.

Фигура, изображенная на рисунке 4.6, б, не является треугольником. Действительно, если ее рассматривать как три точки, соединенные двумя отрезками, то она не удовлетворяет определению треугольника, если ее рассматривать как три точки, соединенные тремя отрезками (два из них совпадают), то угол всего один.

Чтобы разрешить противоречие, возникшее в связи с вырожденными треугольниками, дадим формально-логическое определение треугольника в более узком смысле.

Геометрическая фигура, представляющий собой систему из трех точек, не лежащих на одной прямой, трех соединяющих их отрезков и трех образованных этими отрезками углов называется треугольником.

Что изображено на рисунке 4.5, г? Это целостный объект, но не треугольник, так как не выделены элементы треугольника (вершины, стороны, углы). Объект, изображенный на рисунке 4.5, г будем называть фигурой тре­угольника.