Реконструкция контактной сети 25 кВ железнодорожной станции Карамбай Горьковской железной дороги для повышения пропускной способности, страница 7

где Т – натяжение несущего троса, даН;  – ветровая нагрузка на контактный провод в режиме максимального ветра, даН/м;  – высота (длина) гирлянды изоляторов. Для гирлянды из четырех изоляторов h = 0,9 м;  – результирующая нагрузка на трос в режиме максимального ветра, даН/м; К – натяжение контактного провода, даН/м.

Станция, главный путь:

Станция, боковой путь:

Определение эквивалентной нагрузки [1, стр. 23]:

 

где  – минимальная длина струны, м. =0,8 м; P_т – ветровая нагрузка на трос в режиме максимального ветра, даН/м.

Станция, главные пути:

Станция, боковые пути:

Определение максимально допустимых длин пролетов [2]:

Станция, главные пути:

Станция, боковые пути:

Окончательно для вычерчивания монтажного плана контактной сети станции в соответствии с условием [2], принимаем следующие длины пролетов: станция главные пути – 68 м, боковые пути – 64 м.

2.3. Расчет анкерного участка полукомпенсированной цепной подвески на главном пути станции и построение монтажных кривых

Для расчета взят анкерный участок – Ιа кн, состоящий из пролетов:

Таблица 2.1.

Длина анкерного участка составляет 1465 м.

Определение эквивалентного пролета [3]:

где l_i – длина i – го пролета в анкерном участке, м; l_ау – длина анкерного участка.

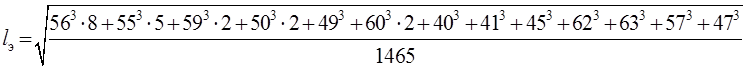
l_э = 56 м.

Определение исходного режима (режима, при котором возможно максимальное натяжение несущего троса)

Определение критического пролета [2]:

где t_г – температура при гололеде. t_г = -5^оС [3]; t_min – минимальная температура, ^оС; Т₀ – натяжение несущего троса при беспровесном положении контактного провода, даН; a – температурный коэффициент линейного расширения материала провода, 1/^оС.

Значение выражения 24a возьмем из [3. табл. 11]:

При Т₀ = Т_max

где Е – модуль упругости провода; S – площадь поперечного сечения провода, мм²; значение aЕS = 18,10 даН/^оС, возьмем из [3, табл. 11].

Так как I_э < I_кр2 (56 м < 95 м), то исходным будет режим минимальной температуры.

Определение точного значения натяжения несущего троса при беспровесном положении контактного провода.

Определяем Т₀, решая уравнение состояния [2]:

где величины с индексом «1» относятся к исходному режиму – режиму минимальной температуры. Для полукомпенсированной подвески К₁ = К [3]:

В этом уравнении неизвестным является Т₀, которое определяется методом подбора.

Т₀ = 1274 даН.

Определение натяжения нагруженного контактным проводом несущего троса в зависимости от температуры для расчетного пролета по уравнению состояния [3]

Величины с индексом «1» – величины исходного режима минимальной температуры. Величины с индексом «х» – величины неизвестного режима, при котором производится расчет проводов. Если не учитывать дополнительные нагрузки, то q_x = g, К_х = К₁ = К [2]. Задаваясь значениями натяжения несущего троса Т_х, будем вычислять соответствующую этому натяжению температуру t_x.

При Т_х = 1960 даН

Данные остальных расчетов сведем в табл.2.2.

Таблица 2.2.

По результатам расчетов строим монтажный график зависимости Т_х(t_х).