3.3 Подбор типовой жесткой поперечины.
Исходные данные.
Подвеска главных путей ПБСМ 95 + МФ 100 на станционных путях ПБСМ 70 + МФ 85. Расчётная толщина стенки гололёда 10 мм, максимальная скорость ветра 25 м/с, длина продольного пролёта 68 м для поперечины 293 – 310. [прил. 3 рис.7]
Расчетная часть.
Для проверки выбираем поперечину типа ОП 180 – 22,5 и определяем расчетные нагрузки.
Нагрузка от собственного веса подвески, даН
Gi = gil + Gт,
где l – длина продольного пролёта, м
gi – нагрузка от веса 1 м подвески, даН/м
Gт – нагрузка от веса конструкции в точке подвеса [3, стр. 193].
Вертикальные силы от подвесок главных путей I и II без гололёда.
Gгл = 1,68 × 68 + 41 = 155,24 даН
Нагрузка от веса гололёда на подвеске, даН
Gгi = gгil,
где gгi – нагрузка от гололёда на 1 м подвески, даН
Gглг = 0,62 × 68 = 42,16 даН
Соответственно вертикальные нагрузки от подвесок станционных путей.
Gст = 1,39 × 68 + 41 = 135,52 даН
Gстг = 0,58 × 68 = 39,44 даН
Нормативные нагрузки от собственного веса 1 м поперечины и от гололёда на 1 м поперечины найдём по [3, табл. 45].
Gp = 31,1 даН и gpг = 10,3 даН/м
Нагрузки на поперечину при ветре максимальной интенсивности и при гололёде. Определим соответственно:
Рр = gU2max, Ррг = g(0,5Umax)2,
где Рр- нагрузка на поперечину от воздействия ветра максимальной интенсивности, даН
Ррг – нагрузка на поперечину от воздействия ветра при гололёде, даН
g - коэффициент [3, табл. 45].
Рр = 0,027 × 252 = 16,87 даН
Ррг = 0,027 × (0,5 × 25)2 =8,44 даН
2.3.1.Определение изгибающего момента в середине пролёта.
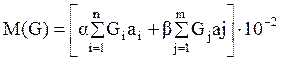, кН·м, [3, стр.191]
где 
и 
коэффициенты,
значения которых приведены в [3, табл. 44].
n и m – число нагрузок, расположенных слева и справа от расчётного сечения
и 
- нагрузки от собственного веса подвесок,
расположенных слева (i) и справа (j)
от расчётного сечения, считая от опоры.
и 
- плечи
нагрузок от собственного веса i и j
Изгибающие моменты от веса гололёда в середине пролёта .
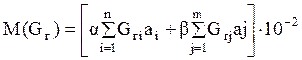, кН·м, [3, стр.191]
где 
и
-
нагрузки от веса гололёда на подвесках, расположенных слева (i)
и справа ( j) от расчётного сечения,
считая от опор.
и 
- плечи
нагрузок от веса гололёда на подвесках i и j
Аналогично моменты для одной трети пролёта составят:
Слева от расчетного сечения
Справа от расчетного сечения
Для дальнейшего расчёта принимаем максимальные из пропущенных моментов, т.е. 20,37 и 4,8 КНм.
Изгибающие моменты от внешних сил в середине пролёта определим:
При аварийном режиме
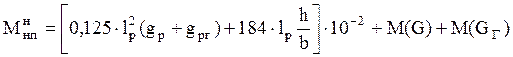, кН·м, [3,
стр.193]
где lp – расчётная длина поперечины, м.
gp и gpг – нагрузки соответственно от собственного веса и от гололёда на 1 м поперечины [3, табл. 45].
h и b – расчётные соответственно высота и ширина поперечины.
При нормальном режиме гололёда с ветром
,
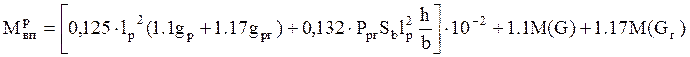где Sв – коэффициент для верхнего пояса учитывающий распределение давления ветра между нижним и верхним поясами поперечины вследствие различной жесткости поясов [3. табл. 42 и 43].
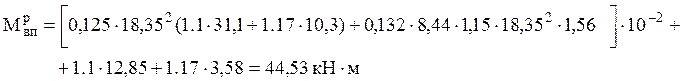
При нормальном режиме максимального ветра.
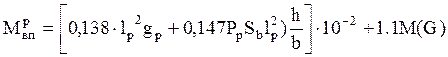, кН·м, [3, стр.193]
Изгибающие моменты в одной трети пролёта:
При аварийном режиме
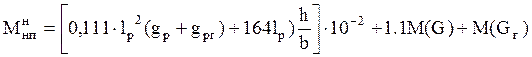, кН·м, [3, стр.195]
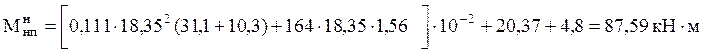
При нормальном режиме гололёда с ветром
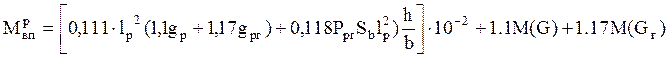
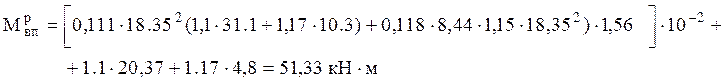
При нормальном режиме максимального ветра
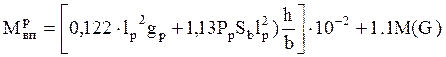, кН·м, [3, стр.195]
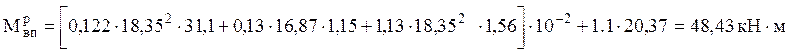Сравнивая максимальные значения полученных
изгибающих моментов от внешних сил с условными допускаемыми, приведёнными [3,
табл. 43], можно сделать вывод о том, что несущая способность принятой к
проверке жесткой поперечины ОП180 – 22,5 удовлетворяет заданным условиям:
В середине пролёта .
= 86,53 кН·м < 163 кН·м
= 44,53 кН·м < 143 кН·м
В одной трети пролёта.
= 87,59 кН·м < 163 кН·м
= 51,33 кН·м < 143 кН·м
2.3.2 Исходные данные для расчёта жёсткой поперечины.
Длина пролёта 56,5 м для поперечины 295 – 312. [прил.3 рис. 7]
Расчётная часть.
Для проверки выбираем поперечину типа ОП 180 – 22,5 и определяем расчетные нагрузки.
Вертикальные силы от подвесок главных путей I и II без гололёда.
Gгл = 1,68 × 56,5 + 41 = 135,92 даН
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.