Оглавление:
Необходимые и достаточные условия ……………………………………… 3
Проценты. Формула сложных процентов ..……………………….………….. 5
Элементы линейной алгебры …………………….………………….………. 10
Элементы комбинаторики ………………..………………….……………….. 43
Задачи для самостоятельного решения. ……………………………...…… 51
Список литературы
Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М., Наука, 1984.
Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М. Наука, 1999.
Ильин В.А., Позняк Э.Г. Линейная алгебра. М., Наука, 1983.
Вариант 9.
1. 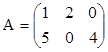 ;
; 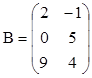 Найти det(AB) и det(BA).
Найти det(AB) и det(BA).
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 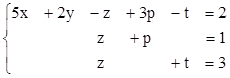 2)
2) 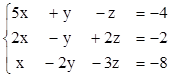
3) 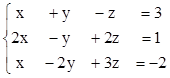 4)
4)
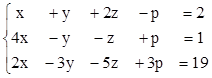
3. Найти ранги матриц. Указать, являются ли строки матриц линейно независимыми. Если не являются, выделить максимально возможное количество линейно независимых строк и оставшиеся строки представить в виде их линейной комбинации.
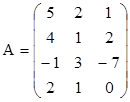 ;
; 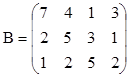
4. Решить матричное уравнение, используя
обратные матрицы. 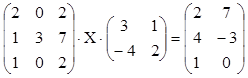
5. Среди данных векторов найти
коллинеарные и ортогональные ![]() =(3,-4,1),
=(3,-4,1), ![]() =(0,1,4),
=(0,1,4), ![]() =(5,5,5),
=(5,5,5),
![]() =(3,3,3).
=(3,3,3).
6. Найти объем параллелепипеда, построенного
на векторах ![]() ,
, ![]() ,
, ![]() из предыдущей задачи, и площадь его
основания.
из предыдущей задачи, и площадь его
основания.
7. Построить область на плоскости: 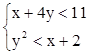 .
.
8. Лежит ли прямая ![]() в
плоскости
в
плоскости ![]() ?
?
59
между собой):
1. Для того чтобы хÎВ, достаточно, чтобы хÎА (если хÎА, то хÎВ).
2. Для того чтобы хÎА, необходимо, чтобы хÎВ (опять, хÎА, то хÎВ). 3. Для того чтобы хÏВ необходимо, чтобы хÏА (если хÏВ, то хÏА).
4. Для того чтобы хÏА, достаточно, чтобы хÏВ (опять, если хÏВ, то хÏА).
Верно и обратное: если выполнено любое из четырех утверждений, то А Ì В.
Запишем условие "если хÎА, то хÎВ" в виде "из А следует В" или "А®В". Понятно, что А можно назвать причиной, В – следствием. Следствие "шире" причины.
Часто при формулировке каких-то условий вместо терминов "необходимо" и "достаточно" используются термины "только тогда" и "тогда".
Тождественными являются утверждения:
"для А необходимо В"
"А выполнено только тогда, когда выполнено В"
"если А, то В"
"из А следует В"
"если ùВ, то ùА"
"из отсутствия В следует отсутствие А"
"для В достаточно А"
"В выполнено тогда, когда выполнено А"
Заучивать наизусть материал этого параграфа не рекомендуется. Надо сопоставить написанное выше с элементарными понятиями русского языка, составить простые примеры для себя лично, и в случае необходимости восстановить в памяти приведенный здесь материал.
Разберем несколько примеров.
1. Четырех угольник называется ромбом, если все его стороны равны.
Четырех угольник называется квадратом, если все его стороны равны, и все его углы – прямые.
Обозначим через А – множество всех квадратов, через В – множество всех ромбов. Очевидно, А Ì В (А есть подмножество В). Следовательно, можно сказать:
- для того чтобы четырехугольник был квадратом, необходимо, чтобы он был ромбом;
- для того чтобы четырехугольник был ромбом, достаточно, чтобы он был квадратом;
- если четырехугольник есть квадрат, то он есть ромб;
- если четырехугольник не есть ромб, то он не является квадратом.
2. Известно, что бабушка ходит в кино только на комедии.
4
Вариант 7.
1. 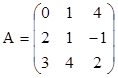 ;
; 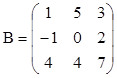 . Найти det(AB), det(B),
det(BA).
. Найти det(AB), det(B),
det(BA).
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 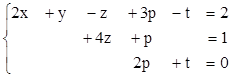 2)
2) 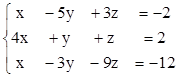
3) 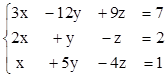 4)
4)
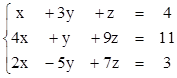
3. Найти ранги матриц. Указать, являются ли строки матриц линейно независимыми. Если не являются, выделить максимально возможное количество линейно независимых строк и оставшиеся строки представить в виде их линейной комбинации.
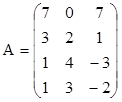 ;
; 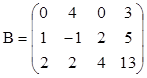
4. Решить матричное уравнение, используя
обратные матрицы. 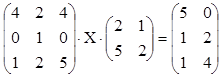
5. Среди данных векторов найти
коллинеарные и ортогональные ![]() =(3,4,-1),
=(3,4,-1), ![]() =(2,-1,3),
=(2,-1,3), ![]() =(1,1,7),
=(1,1,7),
![]() =(4,-2,6).
=(4,-2,6).
6. Найти объем параллелепипеда, построенного
на векторах ![]() ,
, ![]() ,
, ![]() из предыдущей задачи, и площадь его
основания.
из предыдущей задачи, и площадь его
основания.
7. Построить область на плоскости: 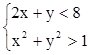 .
.
8. Лежит ли прямая ![]() в
плоскости
в
плоскости ![]() ?
?
57
случае S меньше Т на ![]() %.
%.
Рассмотрим пример:
![]() ; Т=0,8S; S=1,25Т.
; Т=0,8S; S=1,25Т.
Число Т меньше S на 20%, так как
Т составляет 80% от S и за 100% принимается S.
Число S больше Т на 25%, так как
S составляет 125% от Т и за 100% принимаетсяТ.
Получается, что если какую-то величину уменьшили на 20%, то для получения ее снова уменьшенный результат надо увеличить не на 20%, а на 25%.
В том случае, когда используют термин "процент", обязательно указывается, явно или неявно, от какой именно величины процент берется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.