Например, N(a1, a3, a`4) означает количество предметов, обладающих свойствами a1 и a3, и не обладающих свойствами a4. Некоторые из этих предметов обладают свойством a2, которое не указано в скобках, некоторые не обладают – это не важно.
Очевидно, N(a1, a3, a`4)= N(a1, a2, a3, a`4)+ N(a1, a`2, a3, a`4).
Число предметов, не обладающих ни одним из указанных свойств, обозначается по этому правилу N(a`1, a`2, ..., a`m).
Формула включений и исключений имеет вид:
N(a`1, a`2, ..., a`m) = N - N(a1) - N(a2) -...- N(am) + N(a1, a2) + N(a1, a3)+...
...+ N(am-1, am) - N(a1, a2, a3) - N(a1, a2, a4)-...- N(am-2, am-1, am)+...
...+
N(a1, a2, ..., am).
Рассмотрим два примера использования этой формулы.
1. Староста одного класса дал следующие сведения об учениках: "В классе учатся 45 школьников, в том числе 25 мальчиков.
30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18
45
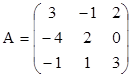. Найти 
.
Решение:
det A=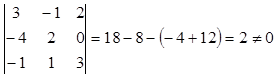
.
|
|
|
|
|
|
|
|
|
|
|
|
Ответ:
.
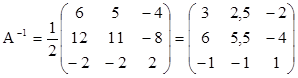При вычислении обратной матрицы легко проверить правильность полученного ответа:
.
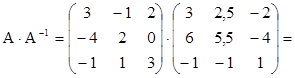
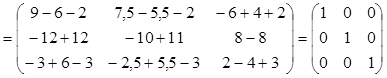Вывод: найдена действительно обратная матрица.
3.4 Ранг матрицы.
Минором матрицы называется определитель ее квадратного остатка, который получается после вычеркивания каких-то строчек, или столбцов, или тех и других. Если размерность квадратного остатка k x k, то определитель этого остатка называют минором k-ого порядка.
18
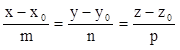- уравнение прямой
через точку М0(х0,у0,z0) и параллельной
вектору 
=(m,n,p).
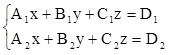- тоже
уравнение прямой (уравнение линии пересечения двух плоскостей)
На плоскости:
Ах+Ву=С – уравнение прямой, вектор 
=(А,В) – перпендикуляр (нормаль) к прямой,
- уравнение прямой
через точку М0(х0,у0) и параллельной вектору =(m,n)
Линейное уравнение первой степени всегда описывает плоскость (в пространстве) или прямую (на плоскости).
Рассмотрим несколько нелинейных уравнений.
В пространстве
- уравнение сферы
радиуса R с центром в точке (х0,у0,z0).
На плоскости
- уравнение окружности
радиуса R с центром в точке (х0,у0).
В пространстве
- уравнение
вертикального кругового цилиндра радиуса R, его ось пересекает
плоскость ХОY в точке (х0,у0,z0).
Замечание:
Линии или поверхности в аналитической геометрии описываются уравнениями. Для описания области на плоскости или в пространстве используют неравенства.
Пример 1.
Найти область на плоскости, заданную неравенством: x+2y>4.
Решение:
Строим линию x+2y=4. Это прямая, для ее построения достаточно подобрать две точки, ей принадлежащие. Например, А (4,0) и В (0,2)
43
Эквивалентными преобразованиями любой матрицы называют следующие действия:
1. перестановка двух любых строк (столбцов);
2. умножение элементов строки (столбца) на число, не равное нулю;
3. вычеркивание одной из двух пропорциональных строк (столбцов);
4. вычеркивание нулевой строки (столбца);
5. сложение элементов любой строки (столбца) с соответствующими элементами другой строки (столбца) умноженными на одно и то же число;
Первая и вторая теоремы позволяют легко определить ранг матрицы, приведя ее эквивалентными преобразованиями к ступенчатому виду.
Пример:
Найти ранг матрицы.
А=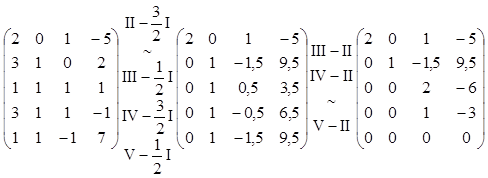
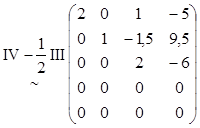
Ответ: r(А)=3.
3.5 Системы линейных уравнений.
Системой линейных уравнений (СЛУ) называется система уравнений вида:
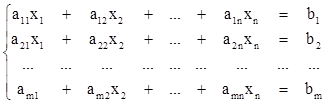, (1)
где 
, 
- известные числа, 
-
неизвестные, i=1,
2, …, m; j=1, 2, …, n;
n
–
количество неизвестных, m – количество уравнений.
Решением СЛУ называется такой набор чисел (х1,х2, …, хn),
20
3.8.1 Две основные задачи аналитической геометрии.
I. Дано описание геометрического образа (линии или поверхности). Найти уравнение этого образа.
Пример 1.
Найти уравнение прямой, проходящей через точку М1 (2,5,-3) и точку М2 (4,1,0).
Решение:
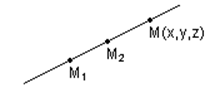
Если точка М(x,y,z)Îпрямой, то 
ôô
, и
наоборот.
=(х-2,у-5,z+3), 
=(2,-4,3).
Условие параллельности векторов и дает
искомое уравнение.
Ответ: 
.
Пример 2.
Найти уравнение плоскости a, проходящей через точку М0(х0,
у0, z0) и перпендикулярной
вектору =(А,В,С).
41
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
