2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 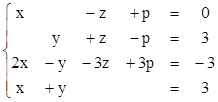 2)
2) 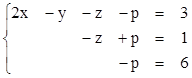
3) 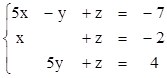 4)
4)
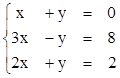
3. Найти ранги матриц. Выделить линейно независимые строки и оставшиеся строки представить в виде их линейной комбинации.
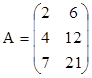 ,
, 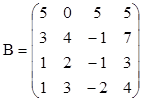
4. Найти обратные матрицы для произведений А×В и В×А, если они существуют.
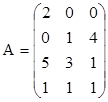 ,
, 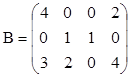
5. Даны координаты вершин пирамиды А(2,1,3), В(1,0,1), С(1,2,6), D(0,0,0). Найти объем пирамиды, длину высоты из вершины А и угол между ребрами АВ и АС.
6. Являются ли вектора ![]() =(3,3,1),
=(3,3,1), ![]() =(3,1,1),
=(3,1,1),
![]() =(9,7,1) компланарными?
=(9,7,1) компланарными?
7. Построить область на плоскости: 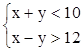 .
.
8. Написать уравнение плоскости, проходящей через точку А(3,5,1) и параллельной плоскости ХOZ.
58
I. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ.
Необходимыми условиями правильности утверждения А называются такие условия, без соблюдения которых утверждение А заведомо не может быть верным.
Достаточными условиями правильности утверждения А называют условия, при которых утверждение А заведомо верно.
Приведем три примера.
1. Необходимым условием делимости целого числа N на 4 без остатка является четность числа N. Условие это необходимо, но не достаточно. Иначе говоря, если число N не является четным, оно не может делиться без остатка на 4, но если число N является четным, то это число может делиться на 4, а может и не делиться.
2. Достаточным условием того, что D АВС – равнобедренный, является условие равносторонности D АВС. Это условие достаточно: если D АВС равносторонний, то он заведомо равнобедренный, но не является необходимым, D АВС может быть равнобедренным, не будучи равносторонним.
3. Необходимым и достаточным условием того, что D АВС – прямоугольный является равенство а2+b2=с2, где а, b, с – длины сторон D АВС, причем с – длина наибольшей стороны.
Из определений необходимого и достаточного условий следует:
1. Если для правильности утверждения А необходимо утверждение В, то для правильности утверждения В достаточно утверждения А.
2. Если для правильности утверждения А достаточно утверждения В, то для правильности утверждения В необходимо утверждение А.
3. Если для правильности утверждения А необходимо утверждение В, то из того, что утверждение А верно, следует, что верно утверждение В: (А®В), и из того, что утверждение В неверно (ùВ), следует, что А также неверно (ùА): (ùВ®ùА).
4. Если для правильности утверждения А достаточно утверждения В, то из того, что утверждение В верно, следует, что верно утверждение А: (В®А), и из того, что утверждение А неверно следует, что и В – неверно: (ùА®ùВ).
5. Если для правильности утверждения А необходимо и достаточно утверждения В, то утверждения А и В тождественны, то есть (А«В), (ùА«ùВ), (АºВ).
Рассмотрим необходимое и достаточное условия принадлежности объекта к какому-то множеству.
] А Ì В, то есть множество А является подмножеством
множества В. Тогда верны следующие утверждения (тождественные
3
Вариант 10.
1. Вычислить определитель матрицы А=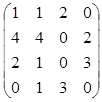 .
.
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 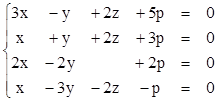 2)
2)
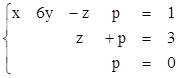
3) 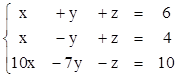 4)
4)
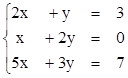
3. Найти ранги матриц. Выделить линейно независимые строки и оставшиеся строки представить в виде их линейной комбинации.
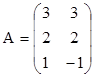 ,
, 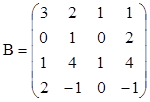
4. Найти обратные матрицы для произведений А×В и В×А, если они существуют.
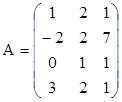 ,
, 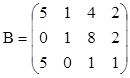
5. Даны координаты трех вершин параллелограмма А(2,1,3), В(1,0,1), С(1,2,6). Найти кооординаты четветой вершины, площадь параллелограмма и угол между диагоналями.
6. Найти вектор, ортогональный векторам ![]() =(4,0,2) и
=(4,0,2) и ![]() =(3,1,1)
=(3,1,1)
7. Построить область на плоскости: 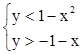 .
.
8. Написать уравнение прямой, проходящей
через точку В(3,2,7) перпендикулярно плоскости ![]() .
.
60
Арцыкова Н.А.
Методические указания к практическим занятиям
по высшей математике
для специальности "экономика"
часть 1
СПбГМТУ
Кафедра математики
2001
Санкт-Петербург
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.