1) Для того, чтобы СЛУ была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы, т.е.
АХ=В совместна Û ![]() .
.
2) Совместная СЛУ будет определенной, если ранг матрицы системы равен рангу расширенной матрицы и равен числу неизвестных, т.е.
АХ=В определенная Û ![]() .
.
3) Если ранги матрицы системы и расширенной матрицы меньше числа неизвестных, то СЛУ является неопределенной со степенью свободы, равной разности числа неизвестных и ранга, т.е.
 .
.
3.5.3 Решение определенных СЛУ по формулам Крамера.
В частном случае, когда СЛУ является определенной и приведена к виду
![]()
(т.е. матрица системы – квадратная и det A¹0), решение СЛУ можно искать по формулам
![]() , j=1, 2, …, n,
, j=1, 2, …, n,
где D= det A (главный определитель СЛУ),
Dj – определитель матрицы, полученной из матрицы А заменой j-того
столбца столбцом правых частей.
Пример1.
Решить СЛУ 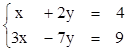 по
формулам Крамера.
по
формулам Крамера.
Решение:
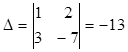 ,
, 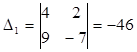 ,
, 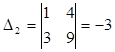 .
.
Ответ: ![]() ,
, ![]() .
.
Пример 2.
26
вектор не меняется, если его переносить параллельно самому себе).
Пример:
Построить вектора ![]() =(2,3),
=(2,3), ![]() =(-4,1) и
=(-4,1) и ![]() =(0,-3)
на плоскости ХОУ.
=(0,-3)
на плоскости ХОУ.
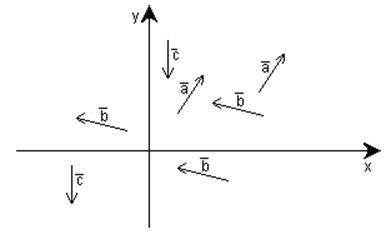
Этот рисунок подчеркивает, что каждый из векторов может быть построен из любой точки, выбранной произвольно.
Вектора принято
обозначать прописными буквами ![]() ,
, ![]() ,
, ![]() и т.п.
или двумя заглавными:
и т.п.
или двумя заглавными: ![]() ,
, ![]() ,
, ![]() и т.п. Вектор обозначают двумя заглавными
буквами, если первая буква – обозначение точки его начала, а вторая –
обозначение точки его конца:
и т.п. Вектор обозначают двумя заглавными
буквами, если первая буква – обозначение точки его начала, а вторая –
обозначение точки его конца:
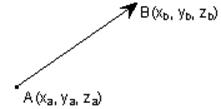
![]() =(xb-xa, yb-ya,
zb-za).
=(xb-xa, yb-ya,
zb-za).
Стандартным базисом в R(2)
служат вектора ![]() =(1,0) и
=(1,0) и ![]() =(0,1), в R(3):
=(0,1), в R(3): ![]() =(1,0,0),
=(1,0,0), ![]() =(0,1,0),
=(0,1,0),
![]() =(0,0,1).
=(0,0,1).
Запись вектора в виде ![]() =а1
=а1![]() +а2
+а2![]() +а3
+а3![]() тождественна записи
тождественна записи ![]() =(а1,а2,а3).
=(а1,а2,а3).
Длина вектора ![]() =(а1,а2,а3)
вычисляется по формуле
=(а1,а2,а3)
вычисляется по формуле
![]() ,
,
а косинусы углов вектора с координатными осями:
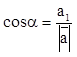 ,
, 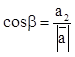 ,
, 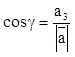 .
.
35
7) a(bх)=(ab)х
8) (a+b)х=aх+bх
Линейным пространством, например, является
множество всех матриц ![]() одинаковой размерности.
одинаковой размерности.
Линейной комбинацией элементов линейного пространства х(1), х(2), …, х(m)ÎХ называют выражение вида
a1х(1)+a2х(2)+…+amx(m) ÎХ,
a1, a2, …, am – произвольные числа.
Чаще всего рассматривают линейное векторное пространство R(n), состоящее из элементов
![]() (х1, х2, …, хn),
(х1, х2, …, хn),
называемых векторами с n координатами. В дальнейшем мы ограничимся рассмотрением только таких пространств.
3.6.1 Линейная зависимость и независимость элементов
линейного пространства.
Элементы ![]() (1),
(1),
![]() (2), …,
(2), …, ![]() (m) ÎХ называются линейно независимыми,
если
(m) ÎХ называются линейно независимыми,
если
a1![]() (1)
+ a2
(1)
+ a2![]() (2)+ …+am
(2)+ …+am![]() (m)=O
(m)=O
только при a1=a2= … =am=0.
Если равенство
a1![]() (1)
+ a2
(1)
+ a2![]() (2)+ …+am
(2)+ …+am![]() (m)=O
(m)=O
может быть выполнено и в том случае, когда хотя бы один коэффициент ai¹0, то элементы называются линейно зависимыми.
Пример 1.
Рассмотрим ![]() =(1,2,5,1),
=(1,2,5,1),
![]() =(0,1,3,1),
=(0,1,3,1), ![]() =(2,3,7,1)
=(2,3,7,1)
2![]() -
-![]() -
-![]() =(2,4,10,2) - (0,1,3,1) -
(2,3,7,1)=(0,0,0,0)=O
=(2,4,10,2) - (0,1,3,1) -
(2,3,7,1)=(0,0,0,0)=O
По определению, ![]() ,
, ![]() ,
, ![]() -
линейно зависимы.
-
линейно зависимы.
Пример 2.
Проверить, являются ли элементы ![]() =(2,5,3),
=(2,5,3), ![]() =(1,0,-1),
=(1,0,-1),
![]() =(5,1,1) линейно зависимыми.
=(5,1,1) линейно зависимыми.
Решение:
Составляем линейную комбинацию элементов и приравниваем ее к нулю.
a![]() +b
+b![]() +g
+g![]() =(2a,
5a, 3a)+(b,
0, -b)+(5g, g,
g)=(2a+b+5g, 5a+g, 3a-b+g)=O
=(2a,
5a, 3a)+(b,
0, -b)+(5g, g,
g)=(2a+b+5g, 5a+g, 3a-b+g)=O
Данное равенство соответствует СЛУ:
28
Легко показать, что 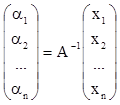 .
.
3.6.4 Скалярное произведение в R(n).
Назовем скалярным
произведением элементов ![]() и
и ![]() Î R(n) число, обозначаемое
Î R(n) число, обозначаемое ![]() ×
×![]() и подчиняющееся следующим требованиям:
и подчиняющееся следующим требованиям:
1) ![]() ×
×![]() =
=![]() ×
×![]()
2) (![]() +
+![]() )×
)×![]() =
=![]() ×
×![]() +
+![]() ×
×![]()
3) (a![]() )×
)×![]() =a×(
=a×(![]() ×
×![]() )
)
4) ![]() ×
×![]() ³0 "хÎ R(n),
причем
³0 "хÎ R(n),
причем ![]() ×
×![]() =0 только для
=0 только для ![]() =O.
=O.
Чаще всего ![]() ×
×![]() вычисляют по формуле
вычисляют по формуле
![]() ×
×![]() =х1у1+х2у2+…+xnyn,
=х1у1+х2у2+…+xnyn,
подразумевая, что ![]() =(х1,
х2, …, xn),
=(х1,
х2, …, xn), ![]() =(у1, у2,
…, yn) в стандартном
базисе.
=(у1, у2,
…, yn) в стандартном
базисе.
Будем называть эту формулу стандартной.
Значение скалярного произведения для двух
фиксированных ![]() и
и ![]() не
должно меняться при изменении базиса, поэтому изменение базиса почти всегда
требует, чтобы изменялась и формула для вычисления скалярного произведения.
не
должно меняться при изменении базиса, поэтому изменение базиса почти всегда
требует, чтобы изменялась и формула для вычисления скалярного произведения.
Скалярное произведение в пространстве R(n)
позволяет ввести понятие длины элемента ![]() и угла между
и угла между ![]() и
и ![]() .
.
В R(2) и R(3)
эти понятия обретают привычный геометрический смысл, так как "![]() ÎR(2) или
ÎR(2) или ![]() ÎR(3) можно рассматривать как
геометрический вектор: отрезок, имеющий определенную длину и определенное направление
по отношению к координатным осям.
ÎR(3) можно рассматривать как
геометрический вектор: отрезок, имеющий определенную длину и определенное направление
по отношению к координатным осям.
Длиной, или нормой ![]() называют число
называют число ![]() ,
,
углом между ![]() и
и ![]() называют угол j, для которого
называют угол j, для которого 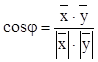 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.