Методические указания к практическим занятиям по дисциплине "Высшая математика". Задачи для самостоятельного решения, страница 8

При использовании стандартной формулы для вычисления × получим:

                                                             33

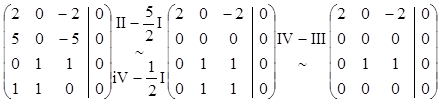
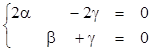
] g=1 ® b=-1, a=1.

-+=O

Вывод: элементы линейно зависимы, =-.

Часто линейную зависимость или независимость набора векторов можно легко проверить, используя следующую теорему:

               Ранг матрицы А равен количеству линейно независимых строк (или столбцов) этой матрицы.

Пример.

Установить являются ли элементы

⁽¹⁾=(2,3,1,0,2)

⁽²⁾=(0,3,1,0,0)

⁽³⁾=(1,0,0,1,1)

⁽⁴⁾=(0,0,0,1,0)

линейно зависимыми.

Решение:

Составляем матрицу А, строки которой – данные элементы и находим ранг этой матрицы.

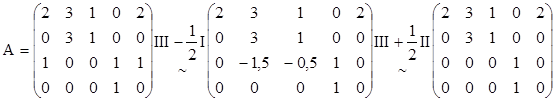
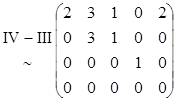
r (A)=3.

Вывод: в наборе только три линейно независимых элемента, а весь набор: ⁽¹⁾, ⁽²⁾, ⁽³⁾, ⁽⁴⁾ – линейно зависим.

               Из последней теоремы следует, что в пространстве R⁽ⁿ⁾ векторов

30

с n координатами любой набор из (n+1) или более элементов будет линейно зависимым, т.к. матрица, составленная из элементов набора, имеет n столбцов и ранг такой матрицы не может быть больше n.

Например, без всякой проверки можно утверждать, что в R⁽²⁾ линейно зависимы любые три элемента.

3.6.2 Базис линейного пространства.

Базисом линейного пространства Х называется набор линейно независимых элементов этого пространства ⁽¹⁾, ⁽²⁾, …, ^(m), такой что " уÎХ  можно представить в виде линейной комбинации базисных элементов:

у=a₁⁽¹⁾ + a₂⁽²⁾+ …+a_m^(m).

Числа (a₁, a₂, …, a_m) называются координатами элемента у в данном базисе, количество базисных элементов m называют размерностью пространства Х.

               В пространстве R⁽ⁿ⁾ c элементами вида =(х₁, х₂, …, х_n) любой базис должен содержать ровно n элементов, и размерность такого пространства равна n.

Запись =(х₁, х₂, …, х_n) подразумевает, что (х₁, х₂, …, х_n) – координаты элемента  в стандартном базисе

=(1,0,0, …,0)

=(0,1,0, …,0)

=(0,0,1, …,0)

…

=(0,0,0, …,1)

При изменении базиса координаты вектора  меняются.

Пример.

Показать, что элементы =(1,2,3), =(-1,2,3), =(0,1,1) образуют базис, и найти координаты =(0,7,11) в этом базисе.

Решение:

, ,  образуют базис, т.к.

1) их количество равно размерности пространства

2) они линейно независимы, ранг матрицы

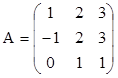 равен трем.

31

Ищем координаты  в этом базисе:

=a+b+g

(0,7,11)=(a- b, 2a+2b+g, 3a+3b+g)

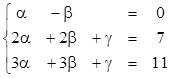  Þ  a=2, b=2, g=-1

=2+2-

Ответ: =(2,2,-1) в базисе , , .

3.6.3 Переход к новому базису.

Обозначим "старый" базис в R⁽ⁿ⁾  - , , …, .

Новый базис - , , …, .

Координаты элементов нового базиса в старом:

=(е₁₁, е₁₂, …, е_1n)

=(e₂₁, e₂₂, …, e_2n)

…

=(e_n1, e_n2, …, e_nn).

А – матрица, столбцами которой являются координаты элементов нового базиса.

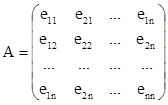
Рассмотрим "=(х₁, х₂, …, х_n), где х₁, х₂, …, х_n – координаты  в старом базисе, т.е. =х₁+х₂+…+x_n.

Требуется найти (a₁, a₂, …, a_n) – координаты  в новом базисе, т.е. представить  в виде =a₁+a₂+ …+ a_n.

32

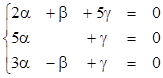
Решая ее методом Гаусса

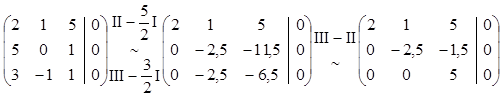
получим равносильную СЛУ

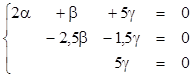
и единственное решение: a=0, b=0, g=0.

Равенство a+b+g=O выполнено только при a=b=g=0.

Вывод: элементы , ,  – линейно независимы.

Замечание: иногда определение линейно зависимых векторов формулируют так:

Элементы ⁽¹⁾, ⁽²⁾, …, ^(m) линейно зависимы тогда и только тогда, когда один из элементов является линейной комбинацией других элементов.

Пример 3.

Проверить,  являются  ли  элементы  =(2, 5, 0, 1),  =(0, 0, 1, 1)  и  =(-2, -5, 1, 0) линейно зависимыми. Если являются, представить один из них как линейную комбинацию других.

Решение:

a+b+g=O

(2a-2g, 5a-5g, b+g, a+b)=(0,0,0,0)

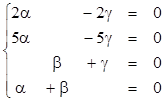
29

, .

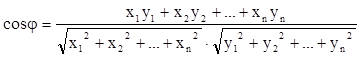Два элемента  и , для которых ×=0, называют ортогональными.

Если среди элементов ⁽¹⁾, ⁽²⁾, …, ^(k) любые два ортогональны, то эти элементы обязательно будут линейно независимы.

Отсюда следует, что любой набор из n взаимно ортогональных элементов будет базисом в R⁽ⁿ⁾. Такой базис принято называть ортогональным.

               Самым "удобным" является ортонормированный базис: базис, в котором базисные элементы не только взаимно ортогональны, но и нормированы, т.е. имеют длину, равную единице.

При переходе от одного ортонормированного базиса к другому формула для вычисления скалярного произведения не меняется.

3.7 Векторная алгебра.