Рассмотрим линейные
пространства векторов с двумя или тремя координатами: R(2) и R(3).
Элемент ![]() =(а1,а2)ÎR(2) можно
рассматривать как направленный отрезок, лежащий в плоскости, а элемент
=(а1,а2)ÎR(2) можно
рассматривать как направленный отрезок, лежащий в плоскости, а элемент ![]() =(а1,а2,а3)ÎR(3) – как
направленный отрезок в прстранстве.
=(а1,а2,а3)ÎR(3) – как
направленный отрезок в прстранстве.
Если на плоскости или в
пространстве задана декартова система координат, то а1=![]() , а2=
, а2=![]() и для
пространственного вектора а3=
и для
пространственного вектора а3=![]() .
.
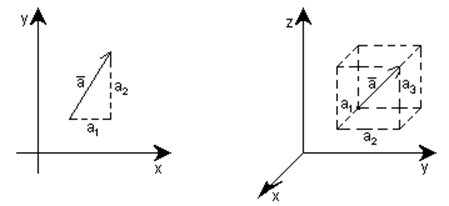
Числа а1, а2, а3 называют координатами вектора. Координаты определяют длину и направление вектора, но не определяют точку его приложения. Два вектора, имеющие одинаковые длины и направления, считаются равными, даже если они приложены в разных точках (т.е.
34
Решить СЛУ 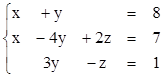 по
формулам Крамера.
по
формулам Крамера.
Решение:
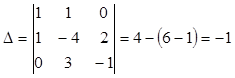
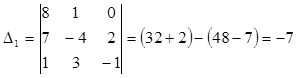 ;
; ![]()
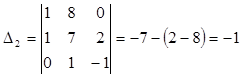 ;
; ![]()
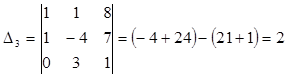 ;
; ![]() .
.
Ответ: х=7, у=1, z=2.
По формулам Крамера, как правило, решают СЛУ с числом неизвестных не больше четырех. Дело в том, что вычисляя главный определитель системы самым рациональным способом, по схеме Гаусса, можно заодно получить и решение СЛУ.
3.6 Линейное пространство.
Рассмотрим некоторое множество Х. Множество называют линейным пространством, если в нем определены действия сложения двух элементов и умножения элемента на число. Эти действия подчиняются следующим правилам:
" x, y, z, … ÎХ и " чисел a, b, …
1) aх ÎХ
2) х+у=у+х ÎХ
3) (х+у)+z=х+(у+z)
4) $ нулевой элемент OÎХ: х+O=O, 0×х=O
5) "х $ противоположный элемент, который принято обозначать (-х): х+(-х)=O
6) 1×х=х
27
(a
- угол ![]() с ОХ, b
- угол
с ОХ, b
- угол ![]() с OY, g - угол
с OY, g - угол ![]() с OZ)
с OZ)
Легко показать, что для любого вектора ![]()
![]() .
.
Рассмотрим два вектора
![]() =(а1,а2,а3)
и
=(а1,а2,а3)
и ![]() =(b1,b2,b3)
(для векторов
=(b1,b2,b3)
(для векторов
![]() =(а1,а2) и
=(а1,а2) и ![]() =(b1,b2) все
аналогично!). Определим их скалярное произведение также как в
пространстве R(n):
=(b1,b2) все
аналогично!). Определим их скалярное произведение также как в
пространстве R(n): ![]() ×
×![]() =а1b1+a2b2+a3b3, но здесь добавим
=а1b1+a2b2+a3b3, но здесь добавим
![]() ×
×![]() =
=![]() ,
,
j
- угол между ![]() и
и ![]() .
.
Отсюда:
1) 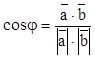
2) условие ортогональности (перпендикулярности) векторов
![]() ^
^![]() Û
Û
![]() ×
×![]() =0 Û
а1b1+a2b2+a3b3=0
=0 Û
а1b1+a2b2+a3b3=0
Два вектора ![]() и
и ![]() будут
линейно зависимы тогда и только тогда, когда они коллинеарны (параллельны).
будут
линейно зависимы тогда и только тогда, когда они коллинеарны (параллельны).
Условие коллинеарности:
![]() ôô
ôô![]() Û
Û
![]() Û
Û
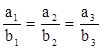
Для двух векторов ![]() =(а1,а2,а3)
и
=(а1,а2,а3)
и ![]() =(b1,b2,b3)
рассматривается операция, не имеющая смысла в R(n) при n¹3: векторное
произведение, которое обозначается
=(b1,b2,b3)
рассматривается операция, не имеющая смысла в R(n) при n¹3: векторное
произведение, которое обозначается ![]() ´
´![]() .
.
![]() =
=![]() ´
´![]() - это вектор со
следующими свойствами:
- это вектор со
следующими свойствами:
1) ![]() ^
^![]() ;
; ![]() ^
^![]()
2) ![]()
3) ![]() ,
, ![]() ,
, ![]() - образуют правую тройку (поворот от
- образуют правую тройку (поворот от ![]() к
к ![]() с конца
с конца
![]() виден против часовой стрелки).
виден против часовой стрелки).
Ясно, что ![]() (площадь
параллелограмма со сторонами
(площадь
параллелограмма со сторонами ![]() ,
, ![]() ).
).
Векторное произведение вычисляется по формуле:
![]() ´
´![]() =
=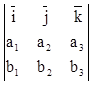 .
.
36
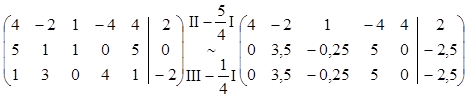
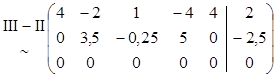
Новая СЛУ, равносильная данной:
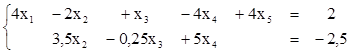
Последнее уравнение выродилось в равенство 0=0, которое выполнено всегда и может быть отброшено.
Рассматриваем уравнение "снизу".
1) в уравнении 3,5х2-0,25х3+5х4=-2,5 три неизвестных. Следовательно, любые два из них можно задать произвольно.
] х2=a, х3=b, тогда
3,5a-0,25b+5х4=-2,5 Þ х4=-0,5+0,05b-0,7a
2) 4х1-2х2+х3-4х4+4х5=2 Þ 4х1-2a+b-4(-0,5+0,05b-0,7a)+4х5=2
или 4х1+4х5=-0,8a-0,8b.
Здесь два неизвестных, одно из них можно задать произвольно.
] х5=g, тогда
4х1+4g=-0,8a-0,8b Þ х1=-0,2a-0,2b-g.
Ответ: 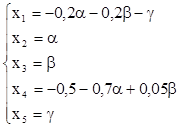
Рассмотренная система имеет бесчисленное множество решений. Для того, чтобы получить конкретное решение, одно из бесчисленного множества, надо задать конкретные значения a, b и g.
При a=5, b=10, g=0 получим
х1=-3, х2=5, х3=10, х4=-3,5, х5=0.
При a=1, b=1, g=1 получим
х1=-1,4, х2=1, х3=1, х4=-1,15, х5=1
и т.д.
Степень свободы системы равна трем.
Все возможные ситуации, которые могут возникнуть при
25
Найти: 1) длины сторон треугольника
2) углы треугольника
3) площадь треугольника.
Решение:
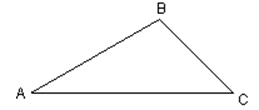
1) найдем координаты векторов, образующих стороны треугольника и их длины
![]() =(-1,1-1);
=(-1,1-1); ![]()
![]() =(-2,6,2);
=(-2,6,2); ![]()
![]() =(-1,53);
=(-1,53); ![]()
2) для определения углов треугольника
воспользуемся формулой 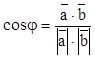 , тогда
, тогда
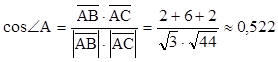 ;
; ![]()
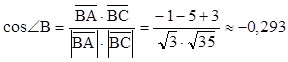 ;
; ![]()
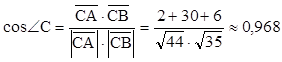 ;
; ![]()
3) для вычисления площади треугольника найдем векторное произведение векторов, образующих любые две его стороны
![]() ´
´![]() =
=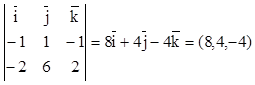
и учтем, что ![]() .
.
![]()
38
3) 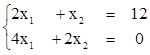 - несовместная СЛУ,
- несовместная СЛУ,
очевидно, что если 2х1+х2=12, то 4х1+2х2=24¹0.
3.5.2 Равносильные СЛУ. Метод Гаусса решения СЛУ.
Две СЛУ называются равносильными, если все решения одной системы являются решениями другой и наоборот.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.