где N – общее число работающих в отделе;
0=N-6-6-7+4+3+2-1 Þ N=11 (в отделе работают 11 человек).
Для ответа на второй вопрос перепишем формулу включений и исключений в виде:
М(a`2, a`3) = М - М(a2) - М(a3) + М(a2, a3),
где М – количество сотрудников, знающих английский язык, знание остальных языков безразлично, или комментируется информацией в скобках.
46
4. Если в определителе поменять местами две любые строки, определитель сменит знак.
5. Если элементы одной из строк определителя умножить на какое-то число, определитель умножится на то же число.
6. Величина определителя не изменится, если к элементам одной из строк определителя прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
Схема Гаусса вычисления определителей порядка n состоит из (n-1) этапа. На первом этапе в матрице определителя на местах элементов а21, а31, ..., аn1 получают нули, не меняя значения определителя. На втором этапе нули получают на местах элементов а32, а42, ..., аn2 и т.д., пока матрица не станет треугольной.
Иллюстрируем схему Гаусса.
Первый этап:
D=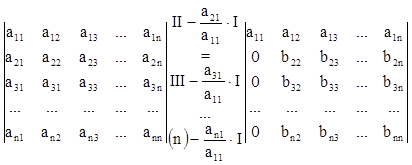
,
где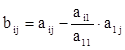 
( i ³ 2, j ³ 2).
На втором этапе "забывают" о существовании первой строки и первого столбца и работают с элементами, обозначенными bij,
D=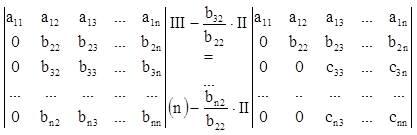
,
где 
( i ³ 3, j ³ 3).
На третьем этапе получаем нули в третьем столбце ниже с33, используя для преобразований третью строку и т.д.
Если окажется, что а11=0 (на первом этапе), или b22=0 (на втором этапе), или с33=0 (на третьем этапе) и т.д., то от этого избавляются, меняя местами строки и, соответственно, знак определителя.
Пример 1: вычислить определитель по схеме Гаусса.
15
Решение:
1) находим число шариков
n=3+2+4=9
2) искомое количество способов
Р(3,2,4)=
.
2.3 Размещения.
Размещением m элементов из n различных называется расположение в определенном порядке каких-либо m элементов из данных различных n элементов. Размещения считаются разными, если они отличаются хотя бы одним элементом или порядком расположения.
Количество различных
размещений обозначается 
и вычисляется по
формуле:
.
Заметим, что в формуле ровно m сомножителей, первый сомножитель равен n, каждый следующий на единицу меньше.
Пример: В турнире участвуют 8 игроков. Каким количеством способов могут распределяться три первых места? (Сколько вариантов "тройки призеров" существует в данном случае?)
Решение: Тройка призеров – это три имени из восьми, расположенные в определенном порядке. Ответом на поставленный вопрос будет число размещений из восьми по три:
.
Можно также рассматривать размещения m элементов из неограниченного количества предметов, относящихся к n различным сортам (предметы одного сорта не различаются).
Размещением с повторениями m элементов из n называется расположение в определенном порядке m предметов из неограниченного количества преметов n различных видов.
Количество таких размещений
обозначается 
и вычисляется по формуле:
.
В этой формуле, также как в
формуле для , ровно m сомножителей, но все
они равны n, а не убывают, как в
предыдущем случае.
Пример: Для запирания сейфа используется замок, который откроется только при наборе на пяти дисках определенных букв. На
48
на "палки" означает, что имеется в виду не матрица, а ее определитель).
Сформулируем правило вычисления определителя, которое не
является его определением, а только следует из определения. Строгое определение определителя матрицы здесь приводить не будем.
]
, (*)
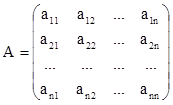
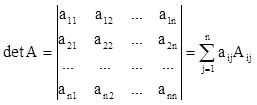где i – номер произвольно выбранной строки (ответ не зависит от выбора i, это доказывается);
- алгебраическое дополнение элемента aij;
Мij – минор – определитель остатка матрицы А после вычеркивания i-ой строки и j-ого столбца.
Равенство (*) сводит вычисление определителя n–ого порядка (порядком
определителя матрицы называют количество строк и столбцов этой матрицы) к
вычислению определителя порядка (n-1). Определитель второго порядка вычисляется
по формуле: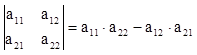 
.
Следовательно, можно при вычислении определителя порядка n перейти к порядку (n-1), затем (n-2), и т.д. до определителей второго порядка.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.