Между (1) и (3) – взаимно-однозначное соответствие. Всегда по виду (3) можно восстановить (1) и наоборот.
Примеры.
1) СЛУ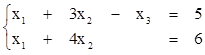 
соответствует матрица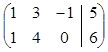 
.
2) Матрице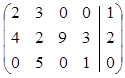 
соответствует СЛУ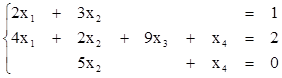 
.
Матрицу СЛУ в условной
записи вида (3) обозначают 
и называют расширенной
матрицей СЛУ.
3.5.1 Типы СЛУ.
СЛУ называется совместной, если она имеет хотя бы одно решение. Совместные системы делятся на определенные, т.е. имеющие одно решение, и неопределенные, имеющие бесконечно много решений. Степенью свободы неопределенной СЛУ называют количество неизвестных, которые можно задать произвольно, после чего значения остальных неизвестных будут определены единственным образом.
СЛУ, не имеющая решений, называется несовместной.
Примеры:
1) 
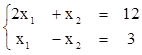- определенная СЛУ,
единственное решение х1=5, х2=2.
2) 
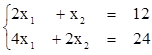- неопределенная СЛУ,
имеет бесконечно много решений х1=a, х2=12-2a, где a - любое число. Например: х1=0, х2=12,
или х1=7, х2=-2,
или х1=-1, х2=14.
и т.д.
Степень свободы системы равна единице.
22
Пример 3.
Найти вектор 
, если
известно, что ^
=(4,2,3), ^
=(1,1,1) и 
=9.
Решение:
Найдем какой-нибудь вектор 
, перпендикулярный и
и, следовательно, параллельный . Проще всего принять =
´.
=
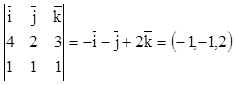
Теперь найдем из
условия: ôô, =9.
Используем условие параллельности векторов в
форме: =l. Отсюда: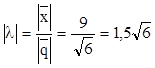 
l=
Ответ: =(1,5
,1,5,-3) или =(-1,5,-1,5,3).
3.8 Элементы аналитической геометрии.
Пусть в R(3) задана декартова система координат с осями ОХ, OY, OZ и уравнение F(x,y,z)=0.
Геометрическим образом уравнения называется множество точек, координаты которых при подстановке в уравнение обращают его в верное равенство.
Пример 1.
Проверить, принадлежат ли точки А (1,1,2) и В
(4,1,0) геометрическому образу уравнения 
.
Решение:
1) подставляем координаты точки А в уравнение: 2=12+12, получаем верное равенство.
2) подставляем координаты точки В в уравнение 0¹42+12, равенство не выполнено.
Ответ: точка А принадлежит геометрическому образу уравнения, точка В – не принадлежит.
Пример 2.
Найти координаты нескольких точек,
принадлежащих геометрическому образу уравнения 
.
Решение:
39
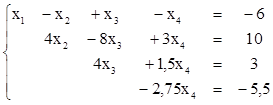
Получим ответ, рассматривая уравнения последовательно "снизу".
-2,75х4=-5,5 Þ х4=2
4х3+1,5х4=3 Þ 4х3+1,5×2=3 Þ х3=0
4х2-8х3+3х4=10 Þ 4х2-8×0+3×2=10 Þ х2=1
х1-х2+х3-х4=-6 Þ х1-1+0-2=-6 Þ х1=-3
Ответ: х1=-3, х2=1, х3=0, х4=2,
или в другой форме: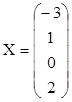 
.
Пример 2.
Решить СЛУ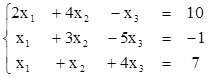 
Решение:
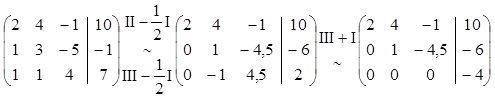
Получена несовместная СЛУ, т.к. последнее уравнение соответствует равенству 0х1+0х2+0х3=4 или 0=4, которое не может быть выполнено. Исходная СЛУ несовместна тоже.
Ответ: СЛУ не имеет решений.
Пример 3.
Решить СЛУ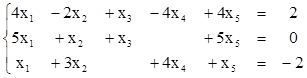 
Решение:
24
Для трех векторов =(а1,а2,а3)
,=(b1,b2,b3)
и 
=(с1,с2,с3),
опять только в R(3), водится операция, называемая смешанным
произведением трех векторов :
=(´)×=×(´).
Смешанное произведение вычисляется по формуле:
=
.
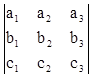>0, если тройка векторов правая,
<0, если тройка векторов левая,
=0, если перемножаемые вектора лежат в
одной плоскости.
Введем понятие компланарности векторов.
Вектора , , , 
, … называюся компланарными, если
они лежат в одной плоскости или параллельных плоскостях.
Два вектора всегда компланарны.
Три вектора компланарны тогда и только тогда, когда они линейно зависимы, или когда их смешанное произведение равно нулю.
Рассмотрим несколько примеров использования векторной алгебры.
Пример 1.
Проверить, лежат ли точки А (2,1,3), В (1,2,2), С (0,7,5), D (-1,4,0) в одной плоскости.
Решение:
Точки лежат в одной плоскости, если вектора 
, 
, 
- компланарны (т.е. лежат в одной
плоскости). Находим координаты этих векторов
=(1-2,2-1,2-3)=(-1,1,-1)
=(0-2,7-1,5-3)=(-2,6,2)
=(-1-2,4-1,0-3)=(-3,3,-3)
и вычисляем их смешанное произведение:
=
.
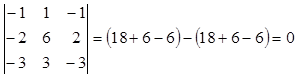Условие компланарности векторов выполнено, , , лежат в одной плоскости.
Ответ: точки А, В, С, D – лежат в одной плоскости.
Пример 2.
Даны координаты вершин треугольника А (2,1,3), В(1,2,2), С(0,7,5).
37
решении СЛУ, описываются в теореме Кронеккера-Капелли, состоящей из трех утверждений:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.