Примеры:
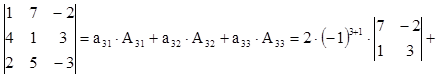
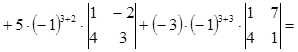
![]()
(при вычислении была выбрана третья строка).
13
![]() ,
,
то есть шесть разных пирожных можно выбрать 924 способами. В последнем примере было поставлено ограничение – разные пирожные. Если же ограничение снять, то количество вариантов выбора возрастет еще больше. Для того чтобы подсчитать количество способов выбора шести любых пирожных из 12 сортов (количество пирожных каждого сорта полагается неограниченным), нужно ввести еще одно определение – сочетание с повторениями.
Рассмотрим неограниченное количество предметов n различных сортов. Пусть предметы одного сорта не различаются. Сочетания с повторениями m элементов из n называется выбор m предметов из неограниченного количества предметов n различных сортов.
Число вариантов выбора или количество таких
сочетаний обозначается ![]() или
или ![]() и
вычисляется по формуле
и
вычисляется по формуле
![]() .
.
Вернемся к задаче о пирожных. Если в магазине имеется 12 сортов пирожных, то шесть пирожных можно купить
![]() способами.
способами.
50
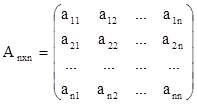
В квадратной матрице выделяют главную диагональ: ее образуют элементы а11, а22, ..., аnn.
Среди квадратных матриц выделяют
- симметричные (относительно главной диагонали): aij=aji.
Например: 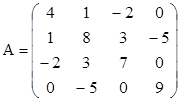 .
.
- верхняя треугольная (нули ниже главной диагонали): aij=0 для всех i>j.
Например: 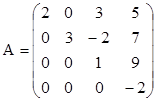 .
.
-нижняя треугольная ((нули выше главной диагонали): aij=0 для всех i<j.
Например: 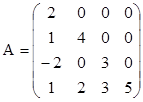 .
.
- диагональная: aij=0 для всех i¹j.
Например: 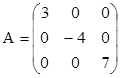
- единичная, которая традиционно обозначается
Е (или I, реже). 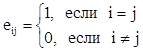 .
.
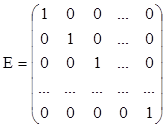 .
.
11
Вариант 2.
1. Вычислить определитель матрицы А=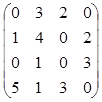 .
.
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 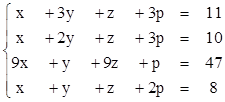 2)
2) 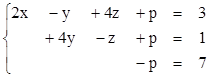
3) 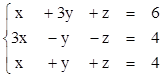 4)
4)
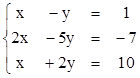
3. Найти ранги матриц. Выделить линейно независимые строки и оставшиеся строки представить в виде их линейной комбинации.
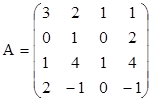 ,
, 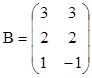
4. Найти обратные матрицы для произведений А×В и В×А, если они существуют.
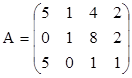 ,
, 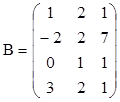
5. Даны координаты вершин треугольника А(2,1,3), В(1,0,1), С(1,2,6). Найти углы треугольника, длины сторон треугольника, площадь треугольника и длину медианы из вершины А.
6. Образуют ли вектора ![]() =(4,0,2),
=(4,0,2), ![]() =(3,1,1),
=(3,1,1),
![]() =(2,5,7) базис?
=(2,5,7) базис?
7. Построить область на плоскости: 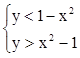 .
.
8. Написать уравнение прямой, проходящей
через точку А(3,5,1) перпендикулярно плоскости ![]() .
.
52
доход составит 3,044562%.)
Максимальный годовой доход (при n®¥) рассчитаем следующим образом:
Сумма ![]() ,
полученная вкладчиком в конце года,
,
полученная вкладчиком в конце года,
![]()
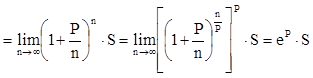 .
.
Абсолютный годовой доход будет равен
![]() ,
,
что составляет ![]() %.
%.
(Если g=20%, годовой доход составит 22,1409%, если g=3%, годовой доход составит 3,045%.)
Заметим, что при g=100%, то есть при
объявленном удвоении "неподвижного" вклада за год, реальный доход
можно довести до ![]() , что составляет 171,828% (на
71,828% больше указанного).
, что составляет 171,828% (на
71,828% больше указанного).
Составим таблицу.
|
% годовых, определяемый банком при "неподвижной сумме" |
% годовых при условии, что каждые три месяца снимаются проценты и добавляются к вкладу |
максимально возможный % годовых при непрерывном снятии процентов |
|
1% |
1,004% |
1,005% |
|
3% |
3,034% |
3,045% |
|
5% |
5,095% |
5,127% |
|
10% |
10,381% |
10,517% |
|
25% |
27,443% |
28,403% |
|
50% |
60,181% |
64,872% |
|
100% |
144,141% |
171,828% |
|
g% |
|
|
Таблица показывает, что, обещая клиентам g% годового дохода и не ограничивая операции с вкладами, банк на самом деле может быть вынужден выплатить более высокий процент. Дополнительный процент
растет вместе с g по закону, проиллюстрированному таблицей. При малых процентных ставках разница не является существенной, но при g=10% она доходит до 0,5%, а при g=50% составляет уже 14,872%, что
9
Вариант 4.
1. Вычислить определитель матрицы А=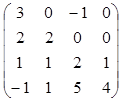 .
.
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 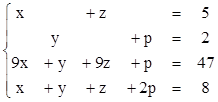 2)
2) 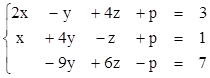
3) 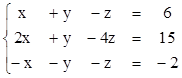 4)
4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.