3. Найти ранги матриц. Выделить линейно независимые строки и оставшиеся строки представить в виде их линейной комбинации.
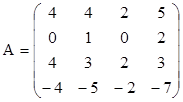 ,
, 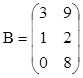
4. Найти обратные матрицы для произведений А×В и В×А, если они существуют.
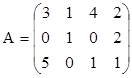 ,
, 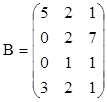
5. Даны координаты вершин треугольника А(2,5,3), В(1,0,1), С(1,4,6). Найти углы треугольника, площадь треугольника и длину высоты из вершины А.
6. Являются ли вектора ![]() =(4,0,2),
=(4,0,2), ![]() =(3,1,1),
=(3,1,1),
![]() =(2,5,7) компланарными?
=(2,5,7) компланарными?
7. Построить область на плоскости: 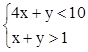 .
.
8. Написать уравнение прямой, проходящей
через точку А(2,5,0) перпендикулярно плоскости ![]() .
.
54
g% увеличить.
Рассмотрим еще одну задачу, связанную с вычислениями процентов от вклада в банк. Задача эта любопытна тем, что в ее решении используется второй замечательный предел
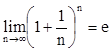 , где е=2,71823.
, где е=2,71823.
В банк положена сумма S. Годовой доход составляет g%. Условия вклада позволяют снять деньги со счета раньше, чем через год, получив не g%, а соответственно меньше: 0,5g% за полгода, 0,25g% за три месяца и т.п.
Все операции
проводятся бесплатно. Вкладчик n раз в год посещает банк, снимает всю сумму
плюс ![]() % от нее, и новую увеличенную сумму опять
кладет в банк.
% от нее, и новую увеличенную сумму опять
кладет в банк.
Требуется ответить на следующие вопросы:
1. Какой процент дохода получит вкладчик к концу года, если будет посещать банк каждые полгода? каждые три месяца? каждую неделю?
2. Какой максимальный процент годового дохода можно получить, посещая банк как можно чаще, например, ежедневно?
Решение:
Введем обозначения:
Р=0,01g; S - сумма, положенная в банк первоначально.
Если вкладчик посещает банк каждые полгода (n=2), то через полгода он получит сумму, равную
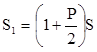 ,
,
через год
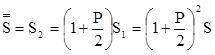 .
.
Годовой доход по абсолютной величине равен 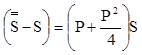 , что составляет
, что составляет 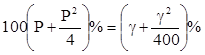 .
.
При n=2 будет получено не g% дохода, а 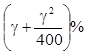 (если g=20%, годовой доход
составит 21%, если g=3%,
годовой доход составит
(если g=20%, годовой доход
составит 21%, если g=3%,
годовой доход составит
7
Вариант 6.
1. Вычислить определитель матрицы А=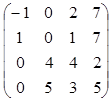 .
.
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 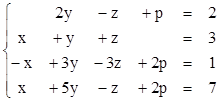 2)
2) 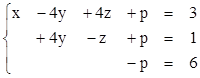
3) 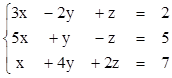 4)
4)
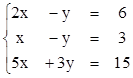
3. Найти ранги матриц. Выделить линейно независимые строки и оставшиеся строки представить в виде их линейной комбинации.
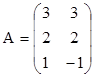 ,
, 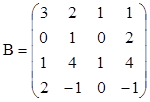
4. Найти обратные матрицы для произведений А×В и В×А, если они существуют.
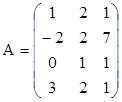 ,
, 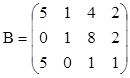
5. Даны координаты вершин пирамиды А(2,1,3), В(1,0,1), С(1,2,6), D(0,0,0). Найти объем пирамиды, длину высоты из вершины D и угол между ребрами АВ и АD.
6. Образуют ли вектора ![]() =(4,5,3),
=(4,5,3), ![]() =(1,-1,2),
=(1,-1,2),
![]() =(2,7,-1) базис?
=(2,7,-1) базис?
7. Построить область на плоскости: 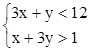 .
.
8. Написать уравнение плоскости, проходящей через точку А(3,5,1) и ось OZ.
56
Следовательно, можно сказать:
- для того чтобы бабушка пошла в кино, необходимо, чтобы там демонстрировали комедию;
- достаточным признаком того, что в зале демонстрируется комедия, является присутствие бабушки;
- если бабушка пошла в кино, то там демонстрируется комедия (но если бабушка не пошла в кино, то там может демонстрироваться что угодно, и комедия, и не комедия);
- если в кинотеатре не идет комедия, то там нет бабушки (но если в кинотеатре идет комедия, то бабушка может, как присутствовать, так и отсутствовать в зале).
II. ПРОЦЕНТЫ. ФОРМУЛА СЛОЖНЫХ ПРОЦЕНТОВ И ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ.
Напомним, что процентом числа S называется сотая часть этого числа.
( 1% от S ) = 0,01 S
( 25% от S ) = 0,25 S
( 80% от S ) = 0,8 S
( 213% от S ) = 2,13 S
( g% от S ) = ![]()
Следует запомнить:
При увеличении числа S на g % получим
![]() .
.
При уменьшении числа S на g % получим
![]() . Если
. Если ![]() , Т составляет (100a)% от S,
, Т составляет (100a)% от S,
S составляет (![]() )% от Т.
)% от Т.
Когда употребляют фразу: "Т меньше S на g %" или "Т больше S на g %", то 1% считают равным 0,01 S, т.е. 1% берется от того числа, которое называют последним.
Поэтому, фраза "Т больше S на g %" не означает, что S меньше Т
на те же g %. Ясно, что Т больше
S на величину D=Т-S, S меньше на Т на ту же величину D, но в первом случае Т больше S на ![]() %, а во втором
%, а во втором
5
Вариант 8.
1. Вычислить определитель матрицы А=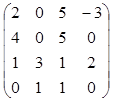 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.