Методические указания к практическим занятиям по дисциплине "Высшая математика". Задачи для самостоятельного решения, страница 4

2. Если определитель содержит строку, целиком состоящую из нулей, то он равен нулю.

3. Если определитель содержит две равные или пропорциональные строки, то он равен нулю.

14

Та же формула может быть представлена в виде:

N(a₁, a`<sub>2</sub>, a`₃) = N - N(a₁) - N(a₁, a₂) - N(a₁, a₃) + N(a₁, a₂, a₃).

Таким образом, число сотрудников, знающих только английский язык, N(a₁, a`<sub>2</sub>, a`₃) найдем следующим образом: N(a₁, a`<sub>2</sub>, a`₃)=6-4-2+1=1 (только английский знает 1 человек).

Аналогично, число сотрудников, знающих только французский

N(a`<sub>1</sub>, a`₂, a₃) = N(a₃) - N(a₁, a₃) - N(a₂, a₃) + N(a₁, a₂, a₃)=7-2-3+1=3.

2.2 Перестановки.

               Перестановкой из n различных элементов называется расположение этих элементов в строго фиксированном порядке. Если в перестановке поменять местами хотя бы два элемента, мы получим уже новую перестановку, не совпадающую с данной.

Ставится вопрос: какое количество различных перестановок можно составить из n различных элементов?

Количество таких перестановок обозначается, как правило,  и находится по формуле

,

где n! = 1×2×3×...×(n-1) ×n – произведение целых чисел от единицы до n.

Пример: Каким количеством способов можно расположить на полке пять разных книг?

Решение: каждая расстановка на полке является перестановкой из пяти элементов, общее количество способов

.

               Перестановкой с повторениями из n элементов, среди которых некоторые элементы одинаковы, называется расстановка этих элементов в определенном порядке, причем, если в такой расстановке поменять местами два одинаковых элемента, перестановка не меняется.

Ставится вопрос: какое количество различных перестановок можно составить из n элементов, среди которых –

n₁ одинаковых предметов первого сорта;

               n₂ одинаковых предметов второго сорта;

               .....................................................................

               n_k одинаковых предметов k-го сорта; и

n₁+n₂+...+n_k=n.

Количество таких перестановок обычно обозначается Р(n₁, n₂, ..., n_k) и находится по формуле:

Р(n₁, n₂, ..., n_k)=.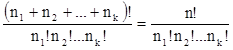

Пример: Каким количеством способов можно расположить в ряд три белых шарика, два красных и четыре черных?

47

Решение:

D=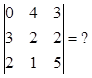

Первый этап:

1) т.к. а₁₁=0, меняем местами первую и, например, третью строки, а также меняем знак определителя по свойству 4; D=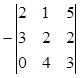

2) требуется получить нули на местах элементов а₂₁ и а₃₁ (а₃₁=0, так что третья строка в преобразованиях не нуждается). Вторую строку преобразуем, отнимая от ее элементов элементы первой строки, умноженные на  (а₁₁=2, а₂₁=3).

Получим: D=.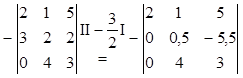

Первый этап закончен.

Второй этап:

b ₂₂=0,5¹0, менять местами ничего не надо. Требуется получить ноль на месте элемента b₃₂. Преобразуем третью строку, отнимая от ее элементов элементы первой строки, умноженные на  (b₂₂=0.5, b₂₃=4).

Получим: D=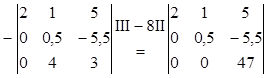

Матрица определителя приведена к треугольному виду.

Ответ: D=.

Пример 2: вычислить определитель по схеме Гаусса.

16

Пусть  –  выбираются два объекта А и В;

            – ни один из способов выбора объекта А не совпадает со способом выбора объекта В, то есть нельзя выбрать А и В одним и тем же способом.

Тогда, если объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор "либо А, либо В" можно осуществить  m+n  способами.

Правило произведения:

Пусть – выбираются два объекта А и В;

           – число способов выбора объекта В не зависит от числа способов выбора объекта А.

Тогда, если объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор пары (А,В) в указанном порядке можно осуществить  m×n  способами.

Правила, эти по природе своей являются определениями и их скорее надо понимать, чем доказывать. Это же замечание относится к формуле включений и исключений.

Формула включений и исключений.

Пусть имеется N предметов, некоторые из которых обладают свойствами a₁, a₂, ..., a_m. При этом каждый предмет может либо не обладать ни одним из этих свойств, либо обладать одним или несколькими свойствами.

               Обозначим через N(a_i, a_j,..., a_k) количество предметов обладающих свойствами a_i, a_j,..., a_k а может быть, и некоторыми другими. Если надо подчеркнуть, что берутся лишь предметы, не обладающие каким-то свойством, это свойство пишем со штрихом.