Рассмотрим задачу:
Число S увеличили на 20%. Результат на 20% уменьшили, получили число Q. Найти отношение чисел S и Q.
Решение: Очевидно, что S¹Q, так как число S увеличивают на 20% от числа S, а полученный результат (обозначим его Р) уменьшают на 20% от этого результата, который не равен S. Учтем, что 20% от любого числа Т равны 0,2Т, тогда
Р=(1+0,2)S=1,2S
Q=(1-0,2)P=0,8P=0,8×1,2S=0,96S
![]()
Ответ: ![]() ,
конечный результат Q составляет 96% от S.
,
конечный результат Q составляет 96% от S.
Комментарий к задаче:
Если в какой-то организации зарплату увеличили на 20%, затем на 20% уменьшили, то зарплата не стала равной первоначальной, а упала по сравнению с ней на 4%.
В общем случае, при увеличении
S
на g%, а затем
уменьшении результата на g%, конечный результат Q будет составлять 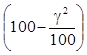 % от S, то есть упадет на
0,01g2%.
% от S, то есть упадет на
0,01g2%.
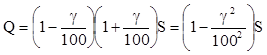 .
.
То же самое получится, если S уменьшить на g%, результат на
6
Вариант 5.
1. 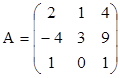 ;
; 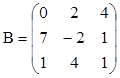 . Найти det(AB), det(B),
det(BA).
. Найти det(AB), det(B),
det(BA).
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 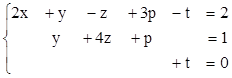 2)
2) 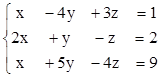
3) 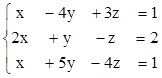 4)
4)
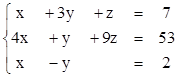
3. Найти ранги матриц. Указать, являются ли строки матриц линейно независимыми. Если не являются, выделить максимально возможное количество линейно независимых строк и оставшиеся строки представить в виде их линейной комбинации.
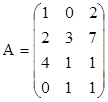 ;
; 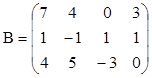
4. Решить матричное уравнение, используя
обратные матрицы. 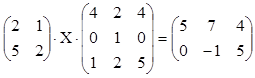
5. Среди данных векторов найти
коллинеарные и ортогональные ![]() =(1,0,-2),
=(1,0,-2), ![]() =(2,4,-1),
=(2,4,-1), ![]() =(8,-5,4),
=(8,-5,4),
![]() =(-4,-8,-2).
=(-4,-8,-2).
6. Найти объем параллелепипеда, построенного
на векторах ![]() ,
, ![]() ,
, ![]() из предыдущей задачи, и площадь его
основания.
из предыдущей задачи, и площадь его
основания.
7. Построить область на плоскости: 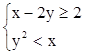 .
.
8. Лежит ли прямая ![]() в
плоскости
в
плоскости ![]() ?
?
55
3,0225%).
Если вкладчик посещает банк каждые три месяца (n=4), то через три месяца он получит
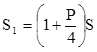 ,
,
через полгода
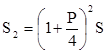 ,
,
через девять месяцев
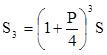 ,
,
через год
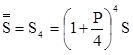 .
.
Годовой доход по абсолютной величине равен
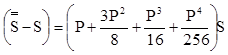 ,
,
что составляет
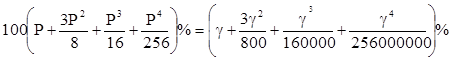 .
.
При n=4 будет получено не g% дохода, а 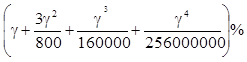 .
.
(Если g=20%, годовой доход составит 21,550%, если g=3%, годовой доход составит 3,034%.)
При посещении банка каждую неделю (n=52), в конце года будет получена сумма
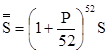 ,
,
что составляет
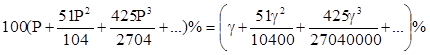 .
.
(Если g=20%, годовой доход составит 22,0934279%, если g=3%, годовой
8
Вариант 3.
1. 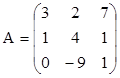 ;
; 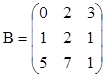 . Найти det(AB), det(A),
det(B), det(BA).
. Найти det(AB), det(A),
det(B), det(BA).
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
1) 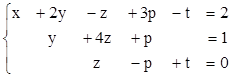 2)
2) 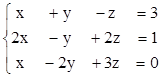
3) 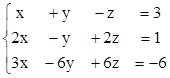 4)
4)
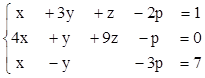
3. Найти ранги матриц. Указать, являются ли строки матриц линейно независимыми. Если не являются, выделить максимально возможное количество линейно независимых строк и оставшиеся строки представить в виде их линейной комбинации.
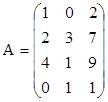 ;
; 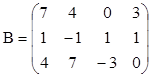
4. Решить матричное уравнение, используя
обратные матрицы. 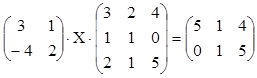
5. Среди данных векторов найти
коллинеарные и ортогональные ![]() =(9,-1,3),
=(9,-1,3), ![]() =(1,12,1),
=(1,12,1), ![]() =(0,3,1),
=(0,3,1),
![]() =(-2,-24,-2).
=(-2,-24,-2).
6. Найти объем параллелепипеда, построенного
на векторах ![]() ,
, ![]() ,
, ![]() из предыдущей задачи, и площадь его
основания.
из предыдущей задачи, и площадь его
основания.
7. Построить область на плоскости: 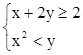 .
.
8. Лежит ли прямая ![]() в
плоскости
в
плоскости ![]() ?
?
53
нельзя оставлять без внимания.
III ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
3.1 Матрицы. Типы матриц. Действия с матрицами.
Матрицей называют прямоугольную таблицу чисел
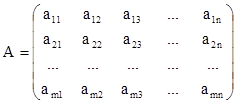 ,
,
![]() - число, стоящее в i-той
строке и j-том столбце.
- число, стоящее в i-той
строке и j-том столбце.
Размерностью матрицы А
называют количество ее строк и столбцов. Записывают размерность матрицы как
индекс: ![]() - матрица, имеющая m строк и n
столбцов.
- матрица, имеющая m строк и n
столбцов.
Условие равенства матриц: равенство размерностей и всех соответствующих элементов
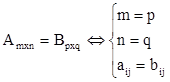 .
.
Типы матриц:
1. Матрица-столбец: 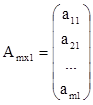 .
.
2. Матрица-строка: ![]() .
.
3. Ступенчатая матрица: каждая строка матрицы кроме, может быть, первой начинается с нуля;
в начале каждой следующей строки нулей больше, чем в предыдущей.
Например: 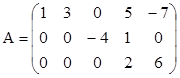 .
.
4. Квадратная матрица: m=n
10
Вариант 1.
1. 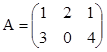 ;
; 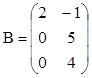 Найти det(AB) и det(BA).
Найти det(AB) и det(BA).
2. Найти решения СЛУ методом Гаусса, указать степень свободы каждой системы. Там, где это возможно, решить СЛУ еще и методом Крамера.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.