Методические указания к практическим занятиям по дисциплине "Высшая математика". Задачи для самостоятельного решения, страница 11

Данная матрица не имеет миноров порядка выше, чем третий.

Рассмотрим миноры третьего порядка для этой матрицы. Все они равны нулю.

,                        ,

,                        .

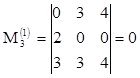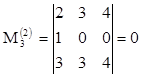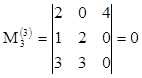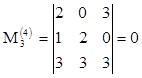Рассмотрим один из миноров второго порядка .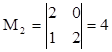

Определение ранга матрицы: Рангом матрицы называется максимальный порядок отличного от нуля минора этой матрицы.

Для рассмотренной выше матрицы rang A=rang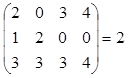, т.е. все ее миноры третьего порядка равны нулю, но $ М₂¹0.

Первая теорема о ранге матрицы:

Ранг ступенчатой матрицы равен числу ненулевых строк.

Пример:

rang, ().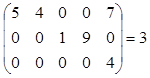

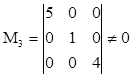Вторая теорема о ранге матрицы:

Эквивалентные преобразования не меняют ранга матрицы.

19

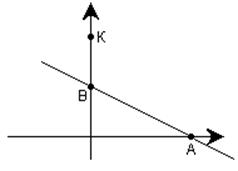
Линия делит плоскость на две части, в одной части x+2y>4, в другой x+2y<4.

Берем любую точку, не лежащую на линии, например точку К (0,4). Подставляя ее координаты в неравенство x+2y>4 получим 0+2×4>4, неравенство выполнено в точке К, и, следовательно в той части плоскости, где точка К находится.

Ответ:

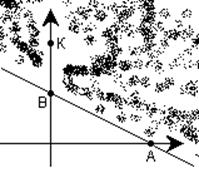
Аналогичным образом строят области, описываемые системами неравенств.

IV. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.

               Представителям самых разных специальностей приходится решать задачи, связанные с подсчетом количества различных комбинаций, подчиненных тем или иным условиям. Подобные задачи могут возникнуть при составлении расписаний, при размещении посевов сельскохозяйственных культур на нескольких полях, при покупке разнообразных предметов и т.п. Понятно, что, в основном, первые задачи комбинаторики касались азартных игр и развивались одновременно с теорией вероятностей.

Приведем основные правила и понятия комбинаторики.

4.1 Общие правила комбинаторики.

Правило суммы:

44

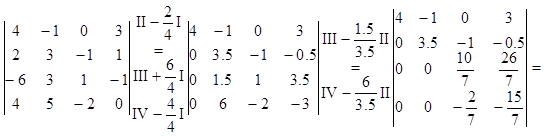
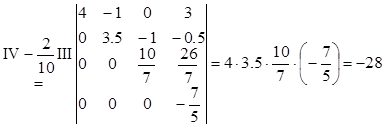
Ответ: D=-28.

3.3 Обратная матрица.

               Обратной матрицей для квадратной матрицы А называется такая матрица В, что .

(Е – единичная матрица, )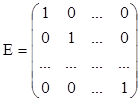

Обратная для  А матрица обозначается . Обратная для А матрица  существует тогда и только тогда, когда det A¹0 (в этом случае матрицу А называют невырожденной). Матрицей, обратной для , является матрица А: .

Обратная матрица вычисляется по формуле:

,

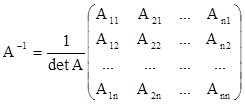где  - алгебраические дополнения элемента  матрицы А.

Следует  обратить  внимание  на  индексы: алгебраические дополнения i-той строки матрицы А расположены в i-том столбце матрицы .

Пример.

17

мальчиков и 17 школьников, учащихся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и в то же время занимаются спортом". Через несколько дней его вызвал к себе классный руководитель (который вел математику) и сказал, что в сведениях есть ошибка.

               Попробуем выяснить, как он это узнал. Для этого подсчитаем, сколько девочек не занимаются спортом и получают время от времени тройки. Обозначим через a₁ принадлежность к мужскому полу, через a₂ – хорошую успеваемость и через a₃ – увлечение спортом. Найдем, чему равно N(a`<sub>1</sub>, a`₂, a`₃). По условию задачи имеем: N(a₁)=25, N(a₂)=30, N(a₃)=28, N(a₁, a₂)=16, N(a₁, a₃)=18, N(a₂, a₃)=17, N(a₁, a₂, a₃)=15. Значит, по формуле включений и исключений получаем, что

N(a`<sub>1</sub>, a`₂, a`₃)=45-25-30-28+16+18+17-15=-2.

Но отрицательным ответ быть не может! Поэтому данные сведения неверны.

               2. В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык. Шестеро знают английский, шестеро – немецкий. Семеро – французский. Четверо знают английский и немецкий, трое – немецкий и французский, двое – французский и английский. Один человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Только французский?

Решение: Ответ на первый вопрос прямым образом получается по формуле включений и исключений. Обозначаем a₁ – знание английского; a₂ – знание немецкого; a₃ – знание французского.

По условию задачи N(a`<sub>1</sub>, a`₂, a`<sub>3</sub>, a`₄)=0 (каждый из работающих знает хотя бы один иностранный язык)

                                    N(a₁)=6, N(a₂)=6, N(a₃)=7;

                                    N(a₁, a₂)=4, N(a₂, a₃)=6, N(a₁, a₃)=2;

      N(a₁, a₂, a₃)=1.

Формула для данной задачи имеет вид:

N(a`<sub>1</sub>, a`₂, a`₃) = N - N(a₁) - N(a₂) - N(a₃) + N(a₁, a₂) + N(a₂, a₃) + N(a₁, a₃) –

- N(a₁, a₂, a₃),