1) 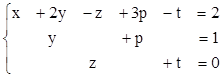 2)
2)
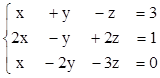
3) 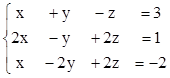 4)
4)
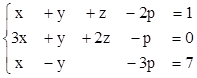
3. Найти ранги матриц. Указать, являются ли строки матриц линейно независимыми. Если не являются, выделить максимально возможное количество линейно независимых строк и оставшиеся строки представить в виде их линейной комбинации.
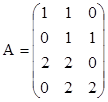 ;
; 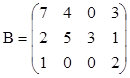
4. Решить матричное уравнение, используя
обратные матрицы. 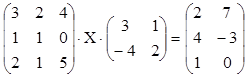
5. Среди данных векторов найти коллинеарные и
ортогональные ![]() =(5,2,1),
=(5,2,1), ![]() =(1,1,-7),
=(1,1,-7),
![]() =(-5,-2,1),
=(-5,-2,1), ![]() =(-2,-2,14).
=(-2,-2,14).
6. Найти объем параллелепипеда, построенного
на векторах ![]() ,
, ![]() ,
, ![]() из предыдущей задачи, и площадь его
основания.
из предыдущей задачи, и площадь его
основания.
7. Построить область на плоскости: 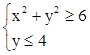 .
.
8. Лежит ли прямая ![]() в
плоскости
в
плоскости ![]() ?
?
51
Действия с матрицами:
1. Транспонирование В=АТ Û bij=aij.
Например: 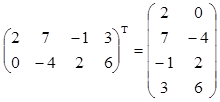 .
.
2. Умножение на число В=aА Û bij=aaji.
3. Сложение двух матриц (операция имеет смысл
только для матриц одной размерности) ![]() Û cij=aij+bij.
Û cij=aij+bij.
4. Умножение двух матриц (операция имеет
смысл только тогда, когда количество столбцов первой матрицы равно количеству
строк второй матрицы) ![]() Û
Û ![]() .
.
(иначе ![]() )
)
Например: 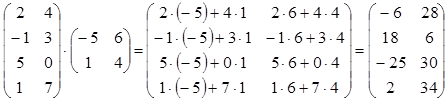 .
.
Справедливо следующее:
1) ![]()
2) А+В=В+А
3) a×(А+В)= aА+aВ
4) А×В¹В×А (как правило). (если А×В=В×А, то А и В называют взаимно перестановочными)
5) А×(В+С)=АВ+АС
6) (АВ)×С=А×(ВС)
3.2 Определитель квадратной матрицы. Схема Гаусса вычисления определителей.
Каждой квадратной матрице
ставится в соответствие число, вычисленное по определенному правилу. Число это
называют "определитель матрицы" и обозначают чаще всего D, det А или 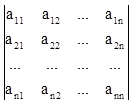 (матрицу
заключают в круглые скобки; замена скобок
(матрицу
заключают в круглые скобки; замена скобок
12
каждом диске 12 букв. Сколько неудачных попыток открыть сейф может быть сделано человеком, не знающим кода?
Число возможных комбинаций
кода в данном случае равно ![]() : мы выбираем 5
элементов – букв из 12 различных (сортов) в определенном порядке, на каждом
диске.
: мы выбираем 5
элементов – букв из 12 различных (сортов) в определенном порядке, на каждом
диске.
![]() .
.
Значит, неудачных попыток может быть 248831.
2.4 Сочетания.
Сочетанием m элементов из n различных называется выборка каких-либо m элементов из данных n элементов без учета порядка. Сочетания считаются разными, если они отличаются хотя-бы одним элементом.
Количество различных сочетаний
обозначается ![]() . Отметим, что из правила произведения
следует:
. Отметим, что из правила произведения
следует:
![]() .
.
Поясним это равенство (его можно считать примером использования правила произведения). Размещение, как было сказано выше, конструируется следующим образом:
- выбирается объект А: m элементов
из n в любом порядке (число способов выбора ![]() )
)
- выбирается объект В: выбранные m элементов
расставляются определенным образом (число способов выбора ![]() ).
).
Следовательно, выбор размещения соответствует
выбору пары объектов АВ и его можно осуществить ![]() способами
и
способами
и ![]() вычисляется по формуле:
вычисляется по формуле:
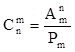 или
или ![]() .
.
Пример: В турнире участвуют 8 игроков. Из трех человек, занявших первые места, формируется команда для поездки на соревнование. Каким количеством способов может быть сформирована команда?
Решение: Вопрос сводится к следующему: каким количеством способов можно выбрать трех человек из восьми? (порядок выбора роли не играет) По определению – это число сочетаний из восьми по три:
![]() .
.
Еще один пример: В магазине 12 сортов пирожных. Покупатель хочет купить шесть разных пирожных. Сколько вариантов выбора у него есть?
49
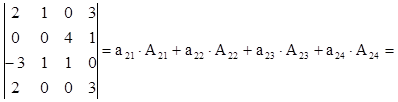
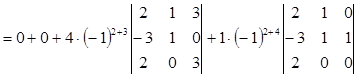
Вычислим два определителя третьего порядка:
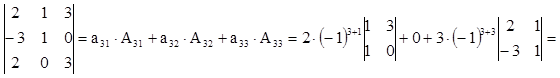
![]()
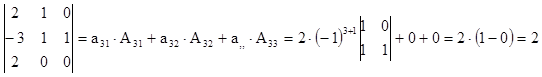
В итоге:
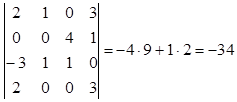
Легко заметить, что для вычисления одного определителя порядка n предложенный алгоритм может потребовать вычисления n×(n-1)×(n-2)× ×...×4×3 определителей второго порядка. (при n=10, например, 1814400 определителей) На практике определители вычисляются по схеме Гаусса. Эта схема позволяет, используя свойства определителей, преобразовать матрицу определителя к треугольной, верхней или нижней, не меняя значения определителя. Определитель же верхней или нижней треугольной матрицы равен произведению диагональных элементов.
Свойства определителей:
1. det A= det АТ (в силу этого все дальнейшие свойства, формулируемые для строк верны и для столбцов)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.