Основные методы теоретического познания, страница 8

          Вид функции можно найти приравнивая правые части вышезаписанных уравнений после их дифференцирования по y:

.

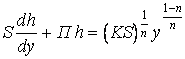          Решим полученное выражение относительно толщины пелены h

.

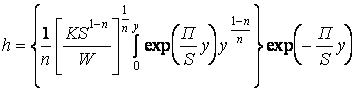          Решение полученного уравнения численным интегрированием методом Симсона позволило установить, что толщина пелены независимо от значения п  по мере подъема фронта потока стремиться к постоянному значению , среднее значение которого составляет 5 мкм и достигает за достаточно короткий промежуток времени . Это означает, что при заполнении реальных полостей форм на зеркале фронта потока при низкой интенсивности турбулентности всегда образует пелена постоянной толщины . При  уравнение имеет аналитическое решение

.

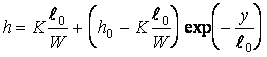          В обобщенных координатах после деления на  оно сводится к виду:                                        ,

где  – безразмерное текущее значение толщины h;

 – начальное безразмерное значение h₀;  – безразмерный симплекс.

          При движении потока алюминиевого или магниевого сплава на ламинарном и переходном режимах течения  толщина оксидной пелены на поверхности сравнительно за короткий промежуток времени достигает своего предельного значения  м не изменяется в дальнейшем по мере продвижения вдоль канала.

          Вторую подзадачу решить аналитически не удается, поэтому можно воспользоваться методом анализа размерностей.

          Загрязненность металла отливок вторичными шлаками Z (мм²/см²) оценивают отношением суммарной площади проекций включения шлака , выявленных при просвечивании рентгеновским излучением, к площади отливки :

.

          Параметр Z можно таким образом принять в качестве оценочного параметра шлакообразующих способностей алюминиевых и магниевых сплавов. Для периода заполнения полости формы расплавом можно принять процесс течения установившемся. В качестве основных геометрических характеристик будем рассматривать искомую величину  и три независимых параметра , , . Динамику процесса определяют силы инерции, трения, тяжести, поверхностного натяжения и давление. Из основного закона динамики  вытекает, что величина  является функцией всех величин, входящих в выражения для расчета всех перечисленных сил , где  – плотность расплава, кг/м³;  – плотность шлака, кг/м³; Р – давление в рассматриваемой точке потока.

          Движение расплава, считая его ньютоновской жидкостью, может быть описано уравнениями Навье - Стокса, не содержащими силы поверхностного натяжения. Кроме того при анализе необходимо учесть временное сопротивление пелены разрыву , Па.