Математика интернациональна и по природе своего развития, не было более динамичной по коммуникабельности отрасли научного знания. Философы считают, что логика природы основана на реализации некоторого относительно небольшого числа фундаментальных законов и закономерностей.
Именно по этому обстоятельству математические методы универсальны по своему характеру и одни и те же уравнения могут быть использованы при решении задач различной природы. Рассмотрим в качестве примера уравнение Лапласа:
, 
,
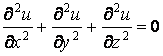где
– некоторая функция координат. Этому
уравнению суждена в теории большая жизнь. Оно с равным успехом может быть
использовано при анализе стационарного теплового состояния однородного тела,
при расчетах распределения электрического заряда на поверхности проводника, в
задаче о движении несжимаемой жидкости. Вариации этого уравнения встречаются и
в теории упругости.
Широкий спектр описательных возможностей имеет уравнение Бесселя:
.
Оно встречается во многих вопросах физики, механики, астрономии.
Казалось бы математика может на своем языке только описать то, что видит человек, т.е. служить способом непосредственного отражения наблюдаемого объекта. Но дело обстоит далеко не так. Математика – это и инструмент опережающего отражения. С ее помощью можно предвидеть феномен, а затем уже найти его.
Самый простой пример тому из теории упругости. Как известно распространение упругого возмущения (S) в полубезграничной среде определяется волновым уравнением
,
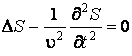где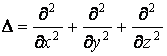 
– оператор
Лапласа.
Рассматривая в рамках
плоской монохроматической задачи решение вида: 
можно
предположить, что существует и решение вида: 
.
И действительно волновое уравнение допускает существование быстро затухающих решений с увеличением z.
|
поверхностных волнах |
Поверхностные волны действительно имеют место и называются волнами Релея и в геодинамических процессах они реально проявляют себя.
Природа образов математики – это сложный философский вопрос он не входит в сферу наших интересов. Значительно более интересно другое. Какую бы сферу жизнедеятельности мы не взяли – физическую теорию, инженерную практику, социально-экономическую ситуацию и др. – в любой из них математика является самым надежным инструментом исследования, дающим самый достоверный результат.
Современная математика дает возможность поставить задачу о самых сложных необычных ситуациях, возникающих в теории надежности, в сфере обслуживания, где пересекаются детерминированные и стохастические ситуации.
Математическое моделирование ситуаций стало частью общей культуры специалиста.
Современная математика представляет собой чрезвычайно разветвленную и в то же время целостную интегрированную область знаний, без опоры на которую в принципе невозможен какой-либо прогресс в науке и технике. Функции математики на современном (компьютерном) уровне развития цивилизации коренным образом изменились по сравнению с классическими схемами прошлого времени, когда математика выполняла пассивную роль инструмента исследований. Современная математика позволила кардинальным образом повысить качество информации сформировала новые методы получения и переработки информации. Наряду с общедоступными методами и «языками» в математике сформировались специальные «языки», специальные методы, используемые узким кругом специалистов и доступные тем, кто работает в узкой области знаний. Это теория групп, методы, используемые в термодинамике, теплофизике, теории упругости, теории нелинейных колебаний и т.п. В наши дни математика значительно расширила свои функции, введя в практику математический эксперимент. Можно реальную физическую систему заменить ее математическим образом и исследовать поведение системы, меняя внешние условия и параметры самой системы. Математический эксперимент выступает как альтернатива пробному физическому эксперименту – это эффективный и экономически выгодный путь научного исследования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
Рис. 12. К задаче о