Размерная функция, описывающая колебательный процесс, в этом случае имеет вид:
![]() .
.
Из теории колебаний известно, что эта задача сводится к решению дифференциальных уравнений [9]
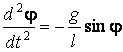 ;
; 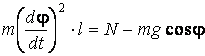 .
.
Начальные условия:
при
t = 0; ![]() и
и ![]() .
.
Это
означает, что за начальный принят момент времени, когда маятник отклонен на
угол ![]() , а скорость его равна нулю.
Основополагаясь на системе уравнений и начальных условиях отметим, что в
качестве определяющих параметров можно принять: t, l, g, m,
, а скорость его равна нулю.
Основополагаясь на системе уравнений и начальных условиях отметим, что в
качестве определяющих параметров можно принять: t, l, g, m,
![]() , где
, где ![]() –
угол отклонения нити в начальный момент времени; t – время. Очевидно,
что в этом случае размерная функция имеет вид
–
угол отклонения нити в начальный момент времени; t – время. Очевидно,
что в этом случае размерная функция имеет вид
![]() .
.
Если учесть, что в этой задаче две зависимые переменные j и N, то можно записать выражения для угла отклонения маятника и силы натяжения нити:
![]() ;
; ![]() .
.
Здесь j и f – безразмерные функции.
С позиции теории подобия функции j и f не зависят от системы единиц измерения. Сам вид функции может быть найден либо решением ранее записанных дифференциальных уравнений или путем постановки целенаправленных опытов.
Записанные выражения имеют три независимых единиц измерения: L, M, T. Тогда в соответствии с p – теоремой получается, что можно составить лишь два безразмерных комплекса
n = m – r = 5 – 3 = 2.
Один из этих безразмерных комплексов очевиден и представляет собой j. Найдем второй. Размерность любой физической величины, характеризующей процесс, можно выразить через первичные размерности:
![]() .
.
Любой безразмерный критерий есть комбинация размерных величин Fi
![]() ,
,
где с – некоторая константа, безразмерная величина, характерная для рассматриваемого процесса.
Перепишем последнее выражение для процесса колебания математического маятника
![]()
или
![]()
Комплексы p должны иметь нулевую размерность. Это будет выполняться, если будет справедливой система уравнений
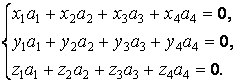
Для вычисления числа независимых решений составим матрицу
 .
.
Пусть r – ранг матрицы размерностей, тогда система имеет (n – r) независимых решений, где n – число существенных величин. В рассматриваемом случае n = 4, а r = 3, т.е. мы можем получить единственное, независимое решение.
На основании записанной матрицы составим систему уравнений
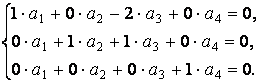
Итак, показатель степени при размерности массы a4 = 0. Т.е. колебания математического маятника не зависят от величины его массы. Перепишем два оставшихся уравнения
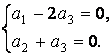
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.