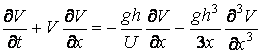Основные методы теоретического познания, страница 6

,

где V – скорость движения частиц жидкости; х – координата; g – ускорение силы тяжести; h – глубина; U – параметр скорости.

          Математический образ этого уравнения в безразмерных переменных обычно представляется в виде:

.

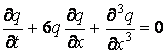          И, наконец, последний пример. В одном из учебных пособий в параграфе, посвященном ударным волнам, энергетическое уравнение приведено в виде:

.

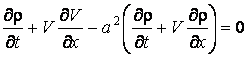          В этом уравнении r – плотность среды, а – скорость звука в ней; остальные обозначения прежние. Даже беглый взгляд укажет на то, что в пособии допущена грубая опечатка, и выглядеть оно должно иначе, а именно:

,

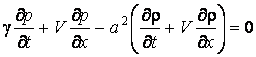где .

          Существенное значение для развития теории имеет мысленный эксперимент. Мысленный эксперимент – это теоретический анализ такой модельной экспериментальной ситуации, которая не может быть воспроизведена в действительности. В качестве примера можно привести мысленный эксперимент Томсона для установления одного из принципов неопределенности.

          Представим себе щель А, на которую падает плоскопараллельный пучок электронов. На экране Э наблюдается дифракционная картина. На этом же рисунке показана зависимость интенсивности дифракционной картины от угла дифракции. Факт прохождения электрона через щель А свидетельствует о том, что неопределенность его координаты  (d – ширина щели). Наиболее интенсивным является первый дифракционный максимум, которому соответствует неопределенность импульса  . Т.к. , а по формуле де Бройля , то получаем

,

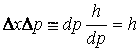откуда следует, что , т.к. оценка в мысленном эксперименте велась по минимуму.

          Мысленный эксперимент успешно «работает» только тогда, когда соединяется с другими методами исследования.

                В качестве  второго примера рассмотрим исследование движения расплава в полости литейной формы, описанное профессором В.В. Чистяковым [45]. Высокая химическая активность к кислороду литейных магниевых и алюминиевых сплавов определяет требования к режиму заливки форм. Интенсивное турбулентное течение расплава обуславливает механическое внедрение (замешивание) оксидов, воздуха и сопутствующих газов внутрь движущегося расплава. Это приводит к образованию в потоке пены и как следствие возникновению одного из наиболее характерных дефектов при литье легких сплавов в виде неметаллических включений, который в литейном производстве принято называть вторичным шлаков.

          Экспериментальные данные Е.М. Ноткина и Н.М. Галдина [46, 47] показали, что образование вторичных шлаков в потоке алюминиевых и магниевых сплавов происходит при числах Re больших чем некоторое характерное значение Re_m

,

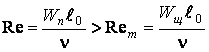где  – максимально допустимая скорость течения расплава в полости формы, после достижения которой образуется вторичный шлак,  – определяющий размер, n – кинематическая вязкость расплава.

          Это может быть объяснено тем, что на ламинарном и переходном режимах течения не происходит течения не происходит разрушения оксидной пленки, а следовательно и отсутствует замешивание ее и воздуха в поток расплава. При превышении характерного числа Re > Re_m пелена теряет устойчивость разрушается периодически обновляясь на поверхности, а сам процесс сопровождается образованием вторичного шлака. Образование вторичных шлаков достаточно сложный процесс и до настоящего времени аналитически не описан. Отсутствуют и адекватные физико-математические модели, что заставило автора [45] решить задачу с использованием метода теории подобия и размерностей. Конечная цель состояла в выявлении закона роста оксидной пелены на поверхности потока при режимах течения, не приводящих к ее разрушению во фронте движущегося потока и произвести критериальную оценку допустимой турбулентности потока на основе использования метода обобщенных переменных.