Основные методы теоретического познания, страница 7

          Поставленную проблему целесообразно разбить на две самостоятельные подзадачи. При решении первой из них автор рассматривает кинетику формирования оксидной пелены на поверхности потока при режимах течения, не приводящих к ее разрыву, т.е. для скоростей течения, удовлетворяющих неравенству .

          Вторая подзадача связана непосредственно со шлакообразованием в турбулентном течении на режимах .

          Проанализируем физику роста оксидной пелены на поверхности потока расплава. Темп поверхностного окисления определяется совокупностью достаточно большого числа факторов: плотности пелены, ее толщины, температуры при которой происходит процесс окисления и т.д. Относительная плотность пелены определяется критерием Пиллинга - Бедвортса [48].

,

где  – объем оксида, образовавшегося при окислении металла, м³;  – объем оксид металла, взятого в определенном массовом количестве, м³.

          При  формируется пористая (рыхлая) пелена, не образующая сплошного плотного покрытия. Следовательно, такая пелена не в состоянии выполнять защитные функции и кислород сравнительно свободно проникает через нее к поверхности текущего расплава металла. Скорость реакции окисления в этом случае практически не зависит от толщины пелены, которая может быть описана зависимостью

,

где h – толщина образующей пелены, м; К_ш – константа скорости химической реакции; t – длительность процесса окисления, с.

          При  образуется защитная (плотная) пелена, затрудняющая диффузию кислорода воздуха к поверхности расплава металла, что приводит к снижению интенсивности ее роста.

          При окислении алюминия образуется пелена из Al₂O₃, для которой , а рост ее толщины подчиняется параболическому закону.

.

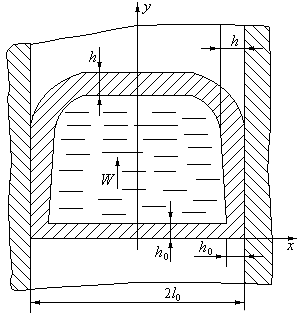
Рис. 10. Схема роста оксидной плены на фронте потока

                Для вывода уравнения процесса формирования оксидной пелены на поверхности потока рассмотрим часть полости формы в виде канала постоянного сечения площадью S со смоченным периметром П. Скорость подъема расплава в форме постоянна. Наличие поперечного градиента скорости по каналу живого сечения приводит к тому, что пелена с боков прижимается к стенке формы, а на свободной поверхности растягивается движущимся потоком постепенно нарастая по мере окисления без разрыва и замешивания (рис.10).

          Для этих условий обобщенная по  зависимость может быть записана в виде

,

где п – показатель стенки зависящий от интенсивности турбулентности потока и плотности пелены.

          Воспользуемся начальными условиями в виде при , толщина пелены составляла . Тогда ее объем за время  равен

.

          Этот объем можно найти интегрированием элементарных объемов по переменной y:

,

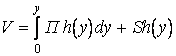где  – функция распределения толщины пелены.