Основные методы теоретического познания, страница 5

          Система из двух уравнений с тремя неизвестными позволяет нам одной из неизвестных задаваться. Пусть а₃ =1, тогда а₂ = –1 и а₁ =2.

          Подставляя, получим безразмерный комплекс

.

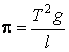          Откуда период Т может быть найден как

.

          Из опыта находим, что константа С =2p и окончательно формула для расчета периода математического маятника примет вид

.

          Более изящный и простой метод основан непосредственно на анализе формулы размерностей. Составим ее для анализируемого случая, предполагая из физических соображений, что . Размерность периода [T], длины [L], ускорения силы тяжести [LT ^-2].

          Формула размерности запишется в виде

,

          откуда получаем, учитывая необходимость соблюдения равенства, что

.

Полученному соотношению размерностей соответствует зависимость

.

          На этом примере мы видим своеобразие применяемого метода: формула величины составлена с точностью до постоянного коэффициента. Для получения точных связей нужны дополнительные данные, позволяющие определить постоянную. Их обычно берут из опытов.

          Несмотря на то, что метод размерностей не является универсальным, тем не менее он нашел широкое применение в гидро-, аэродинамике, тепломассообмене, где строгое решение часто сталкивается со значительными трудностями математического плана, особенно тогда, когда к анализу привлекается значительное число факторов.

          Рассмотрим один пример из гидродинамики: движение волн ряби на поверхности пруда. В формировании процесса важную роль выполняет поле силы тяжести (статически равновесная поверхность жидкости перпендикулярна линиям действия сил гравитации) и капиллярные явления.

          Итак, предполагаем, что скорость распространения волновых движений V от волнового вектора k, плотности жидкости r, коэффициента поверхностного натяжения, s; в выражение для V должно войти также ускорение силы тяжести g.

          Таким образом, . Проведем анализ размерностей:

.

          Т.к. волны на поверхности воды могут образоваться и в таких масштабах, когда роль поверхностных факторов несущественна, то, следовательно, выражение для V должно быть представлено не в виде мультипликативной формы, а в виде аддитивной формы, в которой поверхностный фактор был бы выделен обособленным слагаемым.

          Только единственная форма взаимосвязи определяет величину V:

.

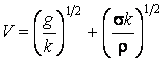          Эта формула, как показывают дополнительные исследования, может быть использована для количественных оценок величины V.

          Выше мы рассмотрели сильные методы научных исследований, без которых современный ученый не работает. Однако следует иметь в виду, что все они являются принципиально ограниченными: модель лишь частично воспроизводит свойства оригинала и не всегда все. Методы теории размерностей и подобия работают успешно только в соединении с теоретическим анализом и экспериментом.

          Теория подобия и размерностей позволяет понять логику уравнений динамики систем, избежать возможных ошибок при их прочтении.

          Рассмотрим распространение волн при малой глубине водоема. Этот процесс описывается уравнением Кортевега-де-Фриза