Система автоматического регулирования температуры воды в деаэраторе ДСА-300, страница 28

Рис.22.

       В момент времени t_i, когда ωt_i=kπ амплитуда колебаний величины Х_к будет иметь значение А_i=A_ke^-mkπ. В момент времени t_i+2, что соответствует ωt_i+2=kπ+2π. Амплитуда

А_i+2=A_ke^-m(kπ+2π).

       Степень затухания ψ – отношение разности двух соседних амплитуд первой из них 

Ψ =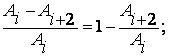

       В соответствии с формулами амплитуд колебаний степень затухания определяется

Ψ = 1 -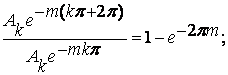  

       Величина 2πm – называется логарифмическим декриментом затухания колебаний

       Различным значениям степени затухания ψ соответствуют

следующие значения величины m:                 Таблица 11.

ψ	0	0,15	0,3	0,45	0,6	0,75	0,9	1
m	0	0,026	0,057	0,095	0,145	0,221	0,366

       При ψ = 0 процесс незатухающий

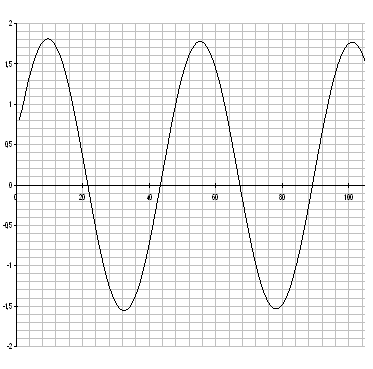
Рис.23.

            при ψ = 1 процесс апериодический

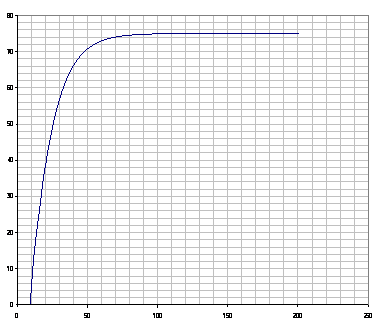
Рис.24.

Все промежуточные значения лежат в 0 < ψ < 1

Наложение ограничений на корень р_к=-mω+iω

 

Рис.25.

tgβ=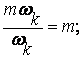

β=arctg m.

       Степень затухания рассматриваемой составляющей процесса будет определяться значением тангенса этого угла. Если корень характеристического уравнения этой системы будет лежать в плоскости комплексного переменного на линии АОВ, то степень затухания Y будет постоянной.

       Выражение передаточной функции звеньев или системы регулирования, для которых корни находятся на линии АОВ, называется расширенной АФЧХ и обозначаются:

;

      Если m=0, то РАФЧХ совпадают с обычными АФЧХ и линия АОВ  совмещается с мнимой осью, следовательно, АОВ – мнимая ось, а система находится на границе устойчивости

 

Рис.26.

т.о. для расчета системы на заданную степень затухания необходимо располагать РАФЧХ объекта и регулятора. Основным уравнением как и при расчете устойчивости будет уравнение

;