Система автоматического регулирования температуры воды в деаэраторе ДСА-300, страница 11

Выбираем максимальную ошибку аппроксимации

= 8,786547%

Вывод: в инженерных расчетах допускается ошибка аппроксимации  ∆<5% , а т.к. максимальная ошибка аппроксимации превосходит 5% (∆_max=8,786547%), отсюда следует, что данный метод не подходит для экспериментальной переходной характеристики.

II способ: пересечение касательной и прямой установившегося значения, дает нам точку из которой мы опускаем перпендикуляр до пересечения с осью абсцисс. Расстояние от точки пересечения касательной с осью абсцисс до точки пересечения перпендикуляра с осью абсцисс равно Т.

              Т = 1,63 мин.

        Составляем передаточную функцию:

             

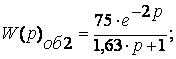
С помощью программы АСОТАР, вводя параметры передаточной функции, найденные ранее (к, τ , Т) строим передаточную характеристику (берем координаты из файла step.num и переносим их в EXCEL для наглядного сравнения характеристик). Расчётный и экспериментальный графики накладываем друг на друга:

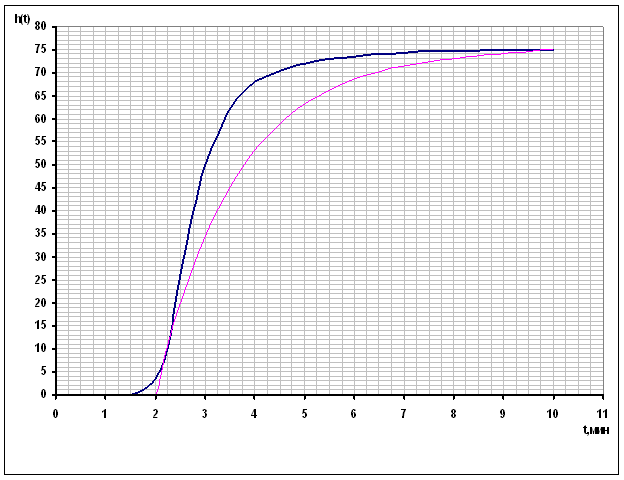
Рис 3. Аппроксимация II способ.

Определяем ошибку аппроксимации для II способа:

                                                          Таблица 3.

2 способ
t	h(t)экс	h(t)расч	Ошибка
	0	0	0
0,25	0	0	0
0,5	0	0	0
0,75	0	0	0
1	0	0	0
1,25	0	0	0
1,5	0,1	0	0,1333333
1,75	1	0	1,3333333
2	3,5	0	4,6666667
2,25	10	10,66435	-0,8858
2,5	26	19,81232	8,25024
2,75	39,6	27,65953	15,920627
3	49,9	34,39094	20,678747
3,25	56,5	40,16519	21,779747
3,5	62	45,1184	22,5088
3,75	65,5	49,36731	21,510253
4	68	53,01205	19,983933
4,25	69,3	56,13855	17,5486
4,5	70,4	58,82048	15,43936
4,75	71,3	61,12107	13,571907
5	72	63,09454	11,873947
5,25	72,5	64,78739	10,28348
5,5	72,9	66,23953	8,8806267
5,75	73,2	67,48519	7,6197467