Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 8

Датчики параметров регулирования    установлены на выходных шинах напряжения  электростанции (эквивалентного генератора). Регулируемым параметром является величина отклонения напряжения на обмотке возбуждения эквивалентного генератора . Нетрудно мысленно представить контур регулирования сильного действия для каждого эквивалентного генератора, мысленно совмести рисунки 1.2.1 и 1.2.2. Структура АРВ-СД и особенности реализации сильного регулирования на каждой станции играют важнейшую роль в обеспечении и повышении устойчивости всей энергосистемы в целом. Этот вопрос является центральным при выполнении курсового проекта «Управление качеством переходных процессов в многосвязных системах управления».

Поскольку основой математического описания при любом  из указанных направлений исследования устойчивости является модель простейшей подсистемы (элемента), то одной из главных задач нашего курса является построение и использование дифференциальных уравнений движения вращающихся машин.

Подробно вопросы традиционного моделирования основного элемента (подсистемы ЭЭС ) в виде эквивалентной вращающейся электрической машины рассмотрены в последующих разделах. На данном этапе изложения материала остановимся на том утверждении, что любую вращающуюся  машину можно описать системой семи известных нелинейных дифференциальных уравнений движения первого порядка (уравнений Горва-Парка) [ ].

Система семи уравнений движения универсальна и описывает установившийся процесс (статику) и переходные процессы (динамику) любой вращающийся машины (синхронный генератор, синхронный двигатель, асинхронный двигатель, обобщенная эквивалентная нагрузка, примыкающая эквивалентная система и др.).

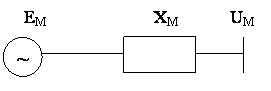
Рис.1.2.3. Эквивалентная схема замещения          Рис. 1.2.4. Схематическое изображение

 любой  вращающейся машины                               системы уравнений Горева - Парка и ркивания из последнего ределителя й точки входа и выхода системы ку любой вращающийся машины(дсистемы), которые бы облада

На рисунке 1.2.3 приведена общая для всех вращающихся машин общая эквивалентная схема замещения. Ее эквивалентными параметрами являются ЭДС (Е_М ), индуктивное сопротивление (Х_М ), и напряжение на шинах статора (U_М). На рис.1.2.4 схематично представлена система уравнений движения машины. Как будет показано ниже, уравнения (1-2) описывают электромагнитные процессы в эквивалентных цепях статорных обмоток, уравнения (3-5) - в обмотках ротора и (6-7) описывают электромеханические процессы движения ротора.

Вернемся к двум направлениям исследования и повышения устойчивости сложных многосвязных систем и рассмотрим два подхода к построению их математических моделей.

Поскольку основной материал данного пособия посвящен методам и анализа и синтеза динамических свойств многосвязных систем использованием приемов глубокого эквивалентирования, то на данном этапе представим лишь обобщенную структурную схему сложной многосвязной системы управления (рис. 1.2.5), позволяющую перейти к простейшему одноконтурному представлению исследуемой системы (рис.1.1.5), что и является результатом глубокого эквивалентирования.

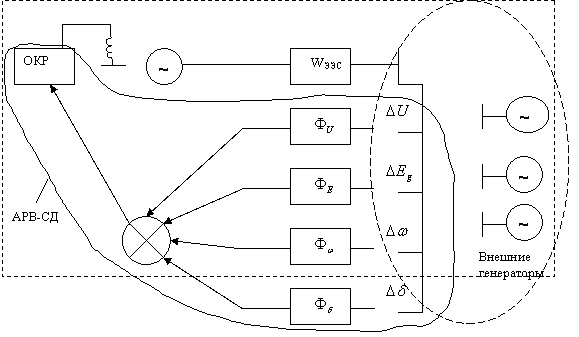
Рис. 1.2.5. Структурное преобразование многосвязной многоконтурной системы в одноконтурную.

На рис. 1.2.5 замкнутая пунктирная линия в виде эллипса указывает на взаимосвязь подсистем; замкнутая ломаная кривая ограничивает функциональные блоки выбранного для настройки АРВ-СД; прямоугольником ограничена вся сложная электроэнергетическая система с учетом многосвязности и многоконтурности за исключением единственного канала регулирования , выбранного для настройки параметров, улучшающих динамические свойства системы. Нетрудно в схеме на рис. 1.2.5 увидеть одноконтурную структурную схему (подобную рис.1.1.5), эквивалентирующую исходную систему относительно выбранного канала регулирования