Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 13

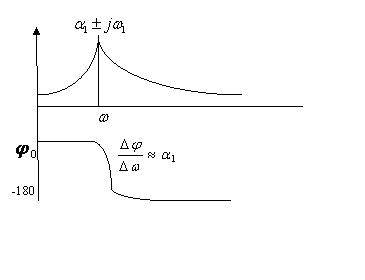
Рис. 1.4.3. Примерный вид АЧХ и ФЧХ, эквивалентирующих сложную систему моделью второго дифференциального порядка

Опыт исследований показывает [ ], что АЧХ и ФЧХ, полученные расчетным путем, при использовании полной математической модели в виде фундаментальной матрицы или путем обработки экспериментальных данных, независимо от сложности системы имеют конфигурацию соответствующую передаточным функциям невысокого (не более 5) порядка. Это объясняется явлением компенсации равных и близких по значению полюсов (корней полинома знаменателя) и нулей (корней полинома числителя соответствующей передаточной функции. Данное явление облегчает задачу параметрической идентификации системы в виде несложной ПФ – выявления нескольких «оставшихся» нескомпенсированных корней знаменателя и числителя.  В частности, амплитудно и фазово- частотные зависимости, приведенные на рис.1.4.3 эквивалентируют систему моделью второго дифференциального порядка. Здесь графики определяются свойствами одной пары комплексно- сопряженных корней, расположенной в знаменателе эквивалентной передаточной функции:

     .                                          (1.4.7)

При анализе колебательной устойчивости наибольший интерес представляют составляющие, соответствующие комплексным нулям и полюсам ПФ. Амплитудные и фазовые частотные характеристики для i-ой комплексно- сопряженной пары корней  имеют вид:

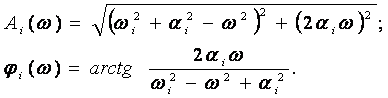                      (1.4.8)      

Из соотношений (1.4.8) следует:  

1) Амплитудно-частотная зависимость комплексной пары полюсов имеет минимум при ча­стоте

 . При этом амплитуда пропорциональна вещественной части корня ;

2) Фазовая характеристика при изменении  от 0 до ∞ получает приращение . Скорость приращения зависит от величины . При   производная зависимости имеет наибольшую величину, которая связана с   соотношением

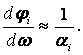                                                                                  (1.4.9)

3) Направление изменения годографа зависит от знака веще­ственной части корня. Приращение фазы   совпадает с ее знаком.

В силу отмеченного первого свойства, минимумы и максимумы характеристики  позволяют локализовать частоты, отвечающие нулям и полюсам с минимальными вещественными частями. В свою очередь известно,  что годограф суммарной ФЧХ на выделенных частотах при оди­наковых, например отрицательных знаках вещественных частей нулей и  полюсов имеет положительное приращение для первых и отрицательное для вторых. Кроме этого, весьма важным для идентификации вещественных частей полюсов и нулей является соотношение (1.4.9), формализующее резонансное свойство ФЧХ. Его можно сформулировать следующим образом: величина вещественной части нуля или полюса на резонансной частоте обратно-пропорциональна скорости изменения фазы. Тем самым возможна количественная оценка отдельных нулей и полюсов.