Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 12

Существуют методы идентификации, позволяющие определять АФЧХ системы между любой парой точек входа и выхода при наличии соответствующих временных выборок сигнала  и  (рис.1.4.2). В их основе лежит использование соотношения связи переменных во временной области в виде интеграла Дюамеля (свертки) входной выборки и весовой функцией системы  (1.4.2). При этом, если  известна , то  установлена однозначная связь между отсчетами входного и выходного сигналов, т.е. известна модель системы в непараметрическом виде (в виде временной выборки) [ ].

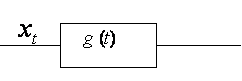
Рис. 1.4.2.  Моделирование системы с использованием весовой функции

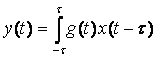                                                                    (1.4.2)

Известно, что свертка выборок во временной области соответствует произведению комплексных изображений этих выборок в частотном спектре (1.4.3).

                                                                  (1.4.3)

Из (1.4.3) следует, что АФЧХ W_з(jω) является частотным изображением весовой функции   и может быть определена отношением спектров выходного и входного сигналов (1.4.4), которые, в свою очередь, могут быть получены путем преобразования Фурье временных выборок реальных сигналов.

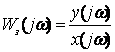    .                                                                                 (1.4.4)

Заметим, что изложенная схема метода определения АФЧХ по выборкам реальных сигналов на практике применима лишь к замкнутым системам, функционирующим с рабочими настройками регуляторов, поскольку размыкание системы для проведения эксперимента недопустимо по соображениям нарушения нормальных условий эксплуатации и, даже потери устойчивости. Данные трудности легко преодолимы при использовании известных прямого и обратного соотношений связи между функциями замкнутой W_з(p). и разомкнутой W_р(p) одноконтурной системы при известном математическом описании и рабочих настройках регулятора Ф_2р.  В частности, для схемы на рис.1.4.1 такими соотношениями для частотных характеристик будут являться (1.4.5- 1.4.6):

                                           (1.4.5)

                                              (1.4.6)

По первому из них может быть рассчитана независимая от настроек характеристика разомкнутой системы при известных характеристиках замкнутой системы W_зр(jω) и регулятора Ф_2р. Второе, при наличии уже известной характеристики разомкнутой системы W_р(jω), используется для выбора новых настроечных параметров  того же регулятора Ф₂, из условия обеспечения желаемых динамических свойств новой замкнутой системы W_з(jω).

Таким образом, результатом непараметрической идентификации является искомая АФЧХ разомкнутой системы. Для проведения этапа параметрической идентификации ее необходимо представить в виде двух действительных выборок: амплитудной частотной (АЧХ) характеристики и фазовой частотной характеристики (ФЧХ) (рис.1.4.3).