Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 15

 - полином  после изъятия из схемы  r –го прямого пути.

Продемонстрируем применение формулы Мейсона на примере схем, приведенных в п.1.1 на рисунках 1.1.4-1.1.5. 

Обоснуем выражение (1.1.9) для передаточной функции  параметра стабилизации Dw (от входа DE_r к выходу Dw ) замкнутой системы (рис.1.1.4). Анализ структуры схемы, приведенной на этом рисунке, выполненный в соответствии с соотношениями (1.5.2-1.5.3) показывает:

- между точками входа (приложения регулирующего воздействия -DE_r ) и выхода (датчика параметра стабилизацииDw) существует единственный прямой путь, определяемый передаточной функцией

     ;                                                  (1.5.4)

- в схеме нет контуров, несоприкасающихся между собой и с прямым путем. Все четыре имеющихся контура - соприкасающиеся со следующими передаточными функциями:

;    ;     ;     ;             (1.5.5)

- исходя из (1.5.2), числитель ПФ строится из выражения:

=;                                                     (1.5.6)

- исходя из (1.5.3) формируется знаменатель:

Δ(p)=1-- - -   .(1.5.7)

Результирующая передаточная функция принимает вид, соответствующий соотношению (1.1.9):

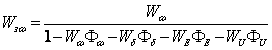    .                                           (1.5.8)

В качестве другого примера применения формулы Мэйсона сформируем передаточную функцию L₁₁(p) параметра ΔТ (от входа DS к выходу DT ) двухконтурной замкнутой системы (рис.1.1.5), тем самым подтвердив корректность выражения 1.1.10.

Выполним по аналогии (1.5.4-1.5.8) исследования структурной схемы (рис.1.1.5):

- между точками входа и выхода существует два прямых пути:

W₁₁(p)   ;           W₁₂ (p) Ф₂ (p) W₂₁ (p)                                 (1.5.9)

- в схеме имеется 3 замкнутых контура:

                                              .            (1.5.10)    

Из них первые два не соприкасаются друг с другом, второй контур не соприкасается с первым путем.

Исходя  из (1.5.2), строим числитель ПФ, - из (1.5.3)  - знаменатель.

В окончательном виде передаточная функция соответствует соотношению (1.1.10):

.                     (1.5.11)

Подчеркнем еще раз, что знаменатели любой передаточной функции построенной для одной схемы будут одинаковыми, независимо от расположения точек входа и выхода, а также прямых путей их соединяющих. Общий знаменатель для всех ПФ схемы является характеристическим полиномом (ХП) системы. Его свойства определяются лишь совокупностью и комбинациями замкнутых контуров (1.5.3). В свою очередь, корни ХП полностью определяют динамические свойства системы. Очевидно, корни и свойства полинома числителя зависят от путей прохождения сигнала в схеме между точками приложения и выхода.