Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 11

По аналогии с (1.3.7-1.3-8) матричный характеристический определитель  может быть представлен характеристическим полиномом = =.

Этот характеристический полином является общим знаменателем для всех передаточных функций системы.

Числитель передаточной функции формируется операторным выражением, зависящим от точки подачи возмущения и точки фиксации сигнала.

Путем вычеркивания из главного характеристического определителя строки возмущаемой и столбца контролируемой переменной может быть получен минор главного определителя, обозначаемый   . Далее, путем поиска собственных чисел соответствующей этому минору матрицы, могут быть получены корни числителя передаточной функции.

                                  (1.3.11)

Поскольку размерность минора ниже размерности главного определителя, порядок числителя реальной передаточной функции всегда на несколько единиц (как минимум на 1) меньше порядка знаменателя.

1.4. Методы построения эквивалентных передаточных функций   для упрощенного моделирования многосвязных систем управления

Как следует из п.1.1 (рис.1.1.5) и п.1.2 (рис.1.2.5) любую многоконтурную многосвязную систему можно строго представить в виде одноконтурной.

Для того, чтобы управлять системой с помощью такой, модели необходимо иметь эквивалентную передаточную функцию системы , разомкнутой по выделенному контуру регулирования  (рис.1.4.1).

 

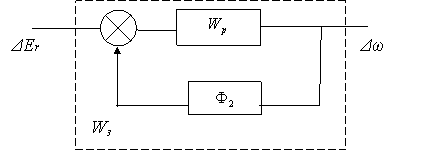Рис. 1.4.1. Одноконтурное представление многосвязной системы с использованием эквивалентной передаточной функции , разомкнутой по каналу регулирования .

 Эквивалентную ПФ можно определить 3-я методами:

1.  с использованием полной модели в виде системы дифференциальных уравнений, если она имеется;

2.  путем идентификации (построение аналитической модели по данным экспериментальных наблюдений);

3. с использованием формулы Мейсона [ ], по математическому описанию структурно входящих в ПФ элементарных звеньев, элементов и подсистем, если оно известно.

Напомним, что первый метод подробно изложен в предыдущем разделе (п.1.3) и заключается в использовании фундаментальной матрицы замкнутой системы для построения главного определителя  и его минора , формируемого вычеркиванием строки и столбца, соответствующих входной и выходной переменным. Окончательно:

 .                                                                             (1.4.1)

Поясним особенности второго пути. Они связаны с использованием для синтеза эквивалентной аналитической модели в виде передаточной функций экспериментальных амплитудно-фазовых частотных характеристик (АФЧХ).

Известно, что по заданной передаточной функции W(p) заменой операторов p=jω (ω=0…∞) может быть получена выборка комплексных чисел W(jω), представляющая соответствующую АФЧХ выходной переменной относительно входной, например для схемы на рис.1.4.1 Δω и ΔEr. В результате идентификации должна быть решена обратная задача – по экспериментально определенной АФЧХ (W(jω)) найдена эквивалентная ПФ W(p).