Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 14

Таким образом, этап параметрической идентификации системы в виде несложной  ПФ сводится к последовательному выявлению действительных и мнимых частей доминирующих (нескомпенсированных) корней числителя и знаменателя. На практике он состоит в выполнении в соответствии с табл.1.4.1 качественного анализа конфигурации АЧХ и ФЧХ, в которых  в разной степени проявляются резонансные свойства различных нулей и полюсов.

Таблица 1.4.1.

Формализация частотных свойств нулей и полюсов, определяющих структуру и количественные характеристики предполагаемой передаточной функции

1	Каждый комплексный полюс имеет резонансный амплитудный пик и наиболее интенсивное изменение фазы на частоте среза. Знак изменения фазы определяется знаком действительной части полюса (для устойчивого звена – отрицательный). Суммарное изменение фазы стремится к величине 180°
2	Каждый действительный полюс имеет падающую АЧХ с максимумом на нулевой частоте и суммарное изменение фазы на 90° во всем частотном диапазоне. Знак изменения фазы совпадает со знаком полюса
3	Каждый комплексный нуль имеет амплитудный минимум и наиболее интенсивное изменение фазы на частоте среза. Знак изменения фазы определяется знаком действительной части полюса (для устойчивого – положительный). Суммарное изменение фазы стремится к величине 180°
4	Каждый действительный нуль имеет монотонно возрастающую  амплитудную характеристику и суммарное изменение фазы на 90° во всем частотном диапазоне. Знак изменения фазы противоположен знаку нуля
5	Величина вещественной части нуля или полюса на резонансной частоте обратно-пропорциональна скорости изменения фазы

Тем самым подробно раскрыта схема второго метода построения эквивалентной ПФ многосвязной системы - путем идентификации.

Основные положения и особенности последнего третьего метода формирования ПФ на основе математического описания входящих в структуру системы элементарных звеньев, элементов и подсистем, ввиду самостоятельной значимости материала  изложены в следующем разделе (п.1.5)

1.5. Построение передаточной функции и характеристического полинома многоконтурной системы управления с использованием формулы Мейсона

Рассмотрим возможность формирования на основе многоконтурного структурного представления системы характеристического полинома общего вида с выделенными искомыми коэффициентами стабилизации:

                                (1.5.1)

С этой целью воспользуемся одним из положений теории графов, а именно, формулой Мейсона [132-134], формализующей процедуру получения выражения для передаточной функции  сложной многоконтурной системы:

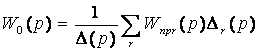.                                 (1.5.2)

Здесь - передаточные функции отдельных прямых путей от входа к выходу схемы, т.е. от входного воздействия к выходной величине;

  ,            (1.5.3)

где     - сумма передаточных функции всех контуров схемы;

 - суммы произведений двух, трех и т.д. передаточных функций контуров, не соприкасающихся друг с другом;