Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 18

1.7. Использование особенностей управляемости и наблюдаемости при эквивалентировании  ЭЭС с несколькими АРВ-СД

Рассмотрим вопрос управляемости и наблюдаемости составляющих движения при эквивалентировании многосвязных ЭЭС.

Под наблюдаемостью составляющей движения системы в частотном спектре будем понимать интенсивность проявления в годографе ЧХ резонансных свойств определенной комплексной пары характеристических корней

.                                              (1.7.1)

соответствующей передаточной функции. Как строго показано в п 1.4 (соотношения 1.4.7-1.4.9), интенсивность резонансных свойств полюса на частоте, близкой к величине мнимой части , тем выше, чем меньше по модулю его вещественная часть , т.е, чем ниже контролируемая нами степень устойчивости. Однако, указанная составляющая, даже при минимальной вещественной части соответствующего полюса, может оказаться ненаблюдаемой или плохо наблюдаемой в случае полной или частичной компенсации данного полюса нулем передаточной функции, имеющим точно такие же или близкие по величине вещественную и мнимую часть. В идеальном случае (при полном количественном совпадении) множитель знаменателя (нуль) и множитель числителя (полюс) передаточной функции взаимно сокращаются, что приводит к полной ненаблюдаемости составляющей в соответсвующих АЧХ и ФЧХ.

 Под управляемостью составляющей движения будем понимать степень эффективности воздействия регулирующего (управляющего) воздействия Ф_i^/ на корни характеристического полинома с малыми вещественными частями.

Очевидно, предлагаемый (в п.1.6) многопараметрический полином D(p), в отношении управляемости во многом эффективнее одноконтурной математической модели, поскольку сформирован по передаточным функциям, в каждой из которых, в общем случае, скомпенсированы различные составляющие движения.

Как следует из особенностей структуры предлагаемой модели, если какая-либо из составляющих движения системы хорошо наблюдаема хотя бы в одной из собственных частотных характеристик W_ii(jw), то она управляемая посредством изменения соответствующих коэффициентов полинома D(p).

Лишь компенсация во всех передаточных функциях W_ij(p) одинаковых групп нулей и полюсов, когда

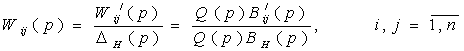       (2.21)

приводит к независимости группы корней характеристического полинома от коэффициентов стабилизации. Например, для двухконтурной структуры:

.   (2.22)

При этом имеет место случай неуправляемости данной группы движений с помощью всей совокупности выделенных станций. Последнее означает слабую связанность выбранной группы станций с оставшейся частью системы и определяет малую эффективность координации параметров стабилизации этих подсистем между собой. Из этих соображений использование многопараметрического полинома для координации настроек наиболее эффективно в случае  сильной взаимной зависимости нескольких выделенных станций. При этом предварительный поиск таких точек регулирования может осуществляться путем анализа совокупности частотных характеристик.

Возвращаясь к вопросу использования полученных частотных характеристик для построения математической модели, отметим, что по   могут быть восстановлены по общей методике (п.1.4) несложные передаточные функции, отражающие основные доминирующие (наблюдаемые) составляющие движения системы. На основе выявленных полиномов числителей и знаменателей формируется модельный многопараметрический полином невысокого порядка, пригодный для параллельной многомерной оптимизации параметров АРВ-СД генераторов нескольких станций.