Экономика и менеджмент \ Многомерные и многосвязные системы управления

Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 5

 ;     ,    т.е.      .                                     (1.1.5)   Корень характеристического полинома нерегулируемой системы λ (знаменателя ПФ разомкнутой системы (p)) полностью определен величиной постоянной времени Tt и не может быть изменен:

    .                                               (1.1.6)

Очевидно, λ  имеет отрицательное действительное значение и определяет вид переходного процесса после возмущения как апериодически затухающий по экспоненциальному закону elt  . При этом интенсивность затухания зависит от величины λ. Соответственно при замыкании  контура регулирования характеристический корень будет определяться из полинома знаменателя замкнутой передаточной функции:

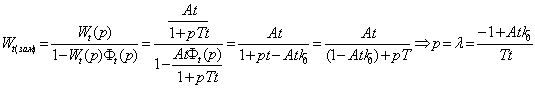.  (1.1.7)

В данном случае, знак и модуль вещественного характеристического корня λ зависят от величины и знака выбранного коэффициента усиления пропорционального регулятора k0. При этом существует однозначная связь: чем больше по модулю отрицательный k0 , тем выше значение функционала качества – степени устойчивости системы. Тем самым представлен простейший пример односвязной системы.

Рассуждения относительно другого автономного (не связанного с первым) контуром регулирования (рис.1.1.1б) приводят к аналогичным выводам об  односвязности соответствующей ему системы.

Заметим, что при незначительных усложнениях передаточной функции объекта и закона регулирования, при отсутствии взаимного влияния нескольких параметров (или сознательном неучете его) система может сохранять свойство односвязности при управлении или регулировании.

Однако реальные  системы управления и их динамические состояния  характеризуются вектором взаимозависимых переменных, что часто приводит к противоречивости влияния на них одного и того же управляющего воздействия.

Рассмотрим более реальный пример регулирования рассмотренного теплового объекта (рис.1.1.1), когда учитывается взаимное влияние выходных параметров   ( изменение температуры теплоносителя) и  (изменение давления теплоносителя). На рисунке 1.1.2 представлен регулируемый объект с параллельным воздействием двух  контуров.

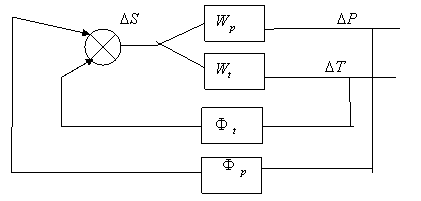
Рис.1.1.2 Регулируемый объект с параллельным воздействием двух  контуров

Двухконтурную схему (рис.1.1.2) можно представить в виде одноконтурной (рис.1.1.3).

 


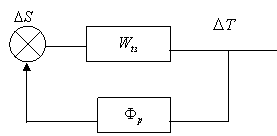Рис.1.1.3 – Неявное представление внутренних контуров в системе

При этом      .

Если в системе управления имеется несколько замкнутых контуров с более сложными законами регулирования, например пропорционально –дифференцирующий, , то многопараметрический характеристический полином включает в качестве искомых настроечных параметров регуляторов несколько пар коэффициентов   .

Тогда характеристический полином можно записать:

Скачать файл