Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 16

1.6.  Обобщенный подход к глубокому эквивалентированию сложных систем управления

Рассмотрим новый подход к моделированию системы произвольной сложности на основе ее обобщенного графоаналитического представления относительно выделенных для настройки контуров стабилизации. В качестве составляющих элементов такого описания предлагается использовать системные собственные и взаимные передаточные функции параметров стабилизации (например, в ЭЭС - отклонения частоты напряжения шин генераторов ) в нескольких точках регулирования. Эти передаточные функции могут быть рассчитаны по исходной системе линеаризованных уравнений или получены экспериментально, как результат идентификации системы.

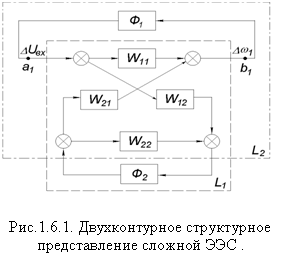На рис.1.6.1 система произвольной сложности структурно представлена через симметрично связанные собственные и взаимные передаточные функции параметров стабилизации нескольких (например, двух) выделенных станций относительно точек замыкания каналов стабилизации. При этом функции W_ij(p), () являются системными, имеющими общий знаменатель D_н(p), и учитывают отсутствие регулирования на выделенных для оптимизации параметров АРВ станциях. Относительно каждого канала стабилизации Ф_i(p), реализующего в АРВ сильного действия закон регулирования по отклонению и производной параметра

                   ,                        (1.6.1)

где P(p)=p/P^//(p) - передаточная функция реального звена дифференцирования в канале стабилизации, оставшаяся часть структурной схемы (на рис.1 показана штриховыми линиями) математически определяется передаточной функцией системы, разомкнутой по данному каналу:

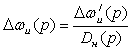                             ,                                                 (1.6.2)

где D_н(p) - характеристический полином нерегулируемой по Dw_u системы; Dw_u^/(p) - полином, полученный из характеристического определителя заменой соответствующего столбца на столбец возмущения, подаваемого в точку замыкания канала стабилизации в АРВ.

Характеристический полином регулируемой системы определяется выражением для структуры со звеном обратной связи :

        .                     (1.6.3)

Граница колебательной устойчивости при p=jw и кривые равного качества (p=-a+jw) могут быть построены путем решения относительно искомых коэффициентов  и  комплексного уравнения D(p)=0.

Предлагаемое графоаналитическое описание позволяет обобщить структурные представления одной и той же сложной системы при разном количестве выделяемых для оптимизации параметров АРВ-СД станций. Так, например, используя структурную схему системы с тремя выбранными станциями (пусть для определенности две из них были учтены в структурных построениях рис.1.6.1), можно получить более подробное выражение для передаточной функции замкнутой системы  того же параметра стабилизации (1.6.2):