Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 4

Рассмотрим подробнее, от чего формально зависит время затухания переходных процессов, а также устойчивость линейной системы, в уравнения движения которой, входят переменные только в первой степени.

Решение линейного неоднородного дифференциального уравнения в общем виде состоит из двух составляющих - вынужденной (установившейся) и  свободной (переходной):

                             x(t)=x_уст(t)+x_пер(t) .                                            (1.1.1)

Здесь - х_уст (t) - частное решение неоднородного уравнения с правой частью, описывающее вынужденный режим системы, устанавливающийся по окончании переходного процесса (например для электрической системы гармонический, с частотой 50 гц.); - x_пер(t) - общее решение однородного уравнения, описывающее переходный процесс в системе, вызванный данным возмущением.

Решение x_пер(t)  однородного дифференциального уравнения, имеет вид:

                            х_пер(t) = С_i e^lit  ,                                                (1.1.2)

где: Ci - постоянная интегрирования, определяющаяся начальными условиями и возмущением; li - корни характеристического уравнения являются комплексными:

    .                                               (1.1.3)

Каждая пара корней дает в выражении (1.2) составляющую переходного процесса, равную:

,               (1.1.4)

где:       

Как видно соотношение (1.4) представляет собой синусоиду (частота bi) с изменяющейся экспоненциально амплитудой. Если a_i<0, то составляющая затухает. Если хотя бы одна составляющая из всех n, где  n - порядок дифференциальной системы уравнений, будет иметь a_i>0, система неустойчива. В частном случае, при b_i =0 , l_i=l_i+1=a_i переходный процесс носит апериодический характер. В соответствии с этим, для линейных систем будем различать  апериодическую и колебательную устойчивость.

Таким образом, суть принятого критерия качества заключается в следующем, чем левее расположен самый правый из комплексных корней (т.е. a_m отрицательное и максимальное по модулю), тем выше скорость затухания суммарного переходного процесса.

Вернемся к определениям односвязности и многосвязности системы.

На рис. 1.1.1 представлены две одноконтурные структурные схемы регулирования двух разных параметров на некотором, например, тепловом объекте.

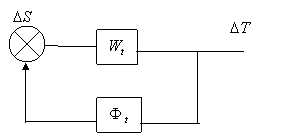
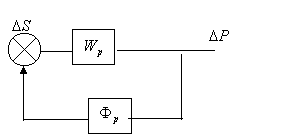
                               а)                                                       б)

Рис. 1.1.1. Одноконтурные структурные схемы регулирования двух разных параметров (на рисунке опущен орепатор «p»

Пусть для схемы на рис. 1.1.1а известны передаточная функция (ПФ) разомкнутой системы (p) от регулирующего воздействия   (например, изменение расхода топлива) к регулируемому параметру   (изменение температуры теплоносителя), а также передаточная функция регулятора в обратной связи (p). Пусть ПФ и закон регулирования будут простейшими: