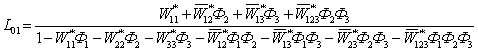Многомерные и многосвязные системы. Управление качеством переходных процессов.: Учебное пособие для курсового и дипломного проектирования, страница 17

 .    (1.6.4)

При этом простота записи достигается использованием найденных выражений для матричных определителей, составленных из собственных и взаимных передаточных функций:                                                   

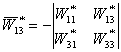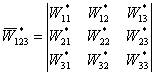  ;             .                 (1.6.5)

Заметим, что в (1.6.4), как и в последующих соотношениях, для сокращения опущен оператор “p”.

Подобным же образом может быть записано и общее выражение для передаточной функции того же параметра стабилизации (L₀₁) при произвольном числе (n) выделенных в системе станций. Из анализа обобщающей формулы Мейсона и соотношений (1.6.4-1.6.5) следует, что при переходе к структурному представлению системы, учитывающему большее на единицу число точек регулирования, необходимо раскрыть структуру каждого элемента исходного графа. Например, для случая с двумя и тремя выделенными станциями указанная связь определяется более подробным описанием собственных и взаимных передаточных функций W_ij, соответствующих двухточечной структуре (рис.1.6.1), через аналогичные W_ij^*,  уже относительно трех выделенных каналов стабилизации:

;

;                                              (1.6.6)

.

Из (1.6.6) следует, что развертывание структуры происходит за счет введения явного описания передаточных функции третьей станции. Поскольку развертывание и сворачивание структуры проводится с использованием общего выражения, независимо от количества контролируемых контуров, определим найденное свойство как рекуррентность структурного представления.

На основании формулы Мейсона и общего ряда контуров по заданным передаточным функциям:

            ,           i,j=1,n  ,                    (1.6.7)

может быть записан искомый характеристический полином D(p) с явно выделенными в нем n- парами коэффициентов стабилизации k_0i, k_1i (i=1,n):

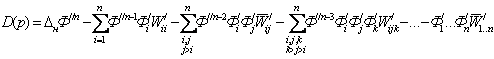.     (1.6.8)

При этом искусственно введенные для упрощения записи взаимные симметричные функции , … формируются минорами, составленными из операторного определителя:

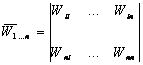, i=1,n.  .                                          (1.6.9)

Подчеркнем, что восстановленный на основе формальных функций  D(p) содержит в виде слагаемых полином с фиксированными коэффициентами Δ_нФ^//n, отражающий свойства нерегулируемой части системы и полиномы, коэффициенты которых являются либо функцией параметров только одного канала стабилизации Ф_i^/ , либо функцией произведения каналов  Ф_i^/ Ф_j^/ (Ф_k^/ ...Ф_n^/).

Отметим, что собственные и взаимные характеристики разомкнутой системы , используемые для формирования многопараметрического полинома с целью координации настроечных параметров АРВ-СД, могут быть получены по аналогии с рассмотренным выше способом (1.4.5-1.4.6), путем обработки результатов эксперимента по получению собственных и взаимных ЧХ (L_0ij) параметра стабилизации замкнутой по всем контурам системы [51].