Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике)

ОГЛАВЛЕНИЕ

1. МНОЖЕСТВА. ОТНОШЕНИЯ НА МНОЖЕСТВАХ

1.1. Основные понятия теории множеств

Множество – совокупность объектов любой природы, называемых элементами данного множества.

Обозначение – большие буквы латинского алфавита для множеств, малые – для его элементов.

Способы задания: 1) перечисление элементов; 2) указание свойства, которым обладают все элементы множества.

Примеры.       1) Множество Х, состоящее из элементов х₁, х₂, х₃, обозначают:

Х = {х₁, х₂, х₃}

              2) Множество простых чисел Х = {x|x - простое число}.

Принадлежность элемента х множеству Х записывается как хÎХ.

Если элемент х не принадлежит Х, то пишут хÏХ.

Множество называется конечным, если оно состоит из конечного числа элемен­тов. Например, множество жителей г. Новосибирска, множество студентов группы ВИ-51.

Множество называется бесконечным, если число его элементов бесконечно. Например, множество натуральных чисел N = {1,2,3,...}.

Бесконечное множество называется счетным, если его элементы можно перечислять. Например, множество натуральных чисел N, множество целых чисел
Z = {...,-3,-2,-1,0,1,2,3,...}.

В противном случае оно называется несчетным. Например, множество точек плоскости, множество вещественных чисел.

Если множество не содержит ни одного элемента, то оно называется пустым и обозначается Æ. Например, пусто множество людей, имеющих рост выше 3 метров. Пусто множество студентов группы ВИ-51, имеющих диплом о высшем образовании.

Множество А называется подмножеством множества В, если любой элемент А является и элементом множества В. Это обозначается так:

АÌВ. Например, множество студентов группы ВИ-51 есть подмножество множества студентов ИСР и НГТУ.

Если множество А является подмножеством множества В и при этом может совпадать с В, то знак Ì подчеркивают: Í.

Множество называется универсальным, если все другие рассматриваемые в данной задаче множества являются его подмножествами. Обозначается такое множество латинской буквой I. Например, если в задаче рассматриваются множество вещественных чисел R, множество целых чисел Z, множество натуральных чисел N и множество рациональных чисел F, то для всех этих множеств множество R является универсальным, так как ZÌR, NÌR и FÌR. Т.е. в данном случае I=R.

1.2. Операции над множествами

1.2.1. Объединение

Обозначение:

Определение. Объединением двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые входят во множество А или во множество В или в оба вместе, причем элементы, принадлежащие обоим множествам одновременно, входят в объединение только один раз.

   Если С = А В, то С = {c| cÎА или сÎВ или сÎА и В одно­временно}.

Операции над множествами можно наглядно изобразить с помощью диаграмм Эйлера-Венна. На этих диаграммах универсальное множество изображается в виде прямоугольника, а множества, участвующие в операции - кругами.

Представление объединения на диаграмме Эйлера-Венна (результат объединения закрашен):

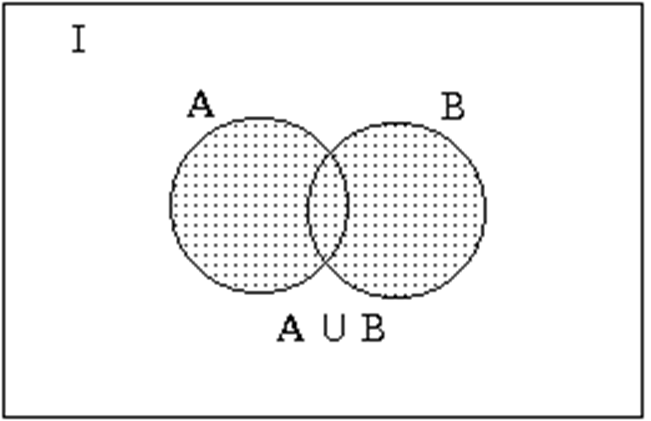
Примеры:

1) А = {a, b, c, d}, B = {c, d, e, f}, C=A B={a, b, c, d, e, f}

2) Z⁺ – множество целых положительных чисел;

  Z^- – множество целых отрицательных чисел;

  О = {0};

  C = Z⁺ Z^- O = Z – множество всех целых чисел.

3) А – множество студентов гр. ВИ-51, учащихся на отлично;

  В – множество студентов гр. ВИ-51, учащихся без троек;

  С – множество студентов гр. ВИ-51, имеющих удовлетворительные оценки;

  D – множество студентов гр. ВИ-51, имеющих неудовлетворительные оценки;

  E = A B C D - множество всех студентов группы ВИ-51.

Свойства: 1) коммутативность (переместительный закон)

               А В = В А

     2) ассоциативность (сочетательный закон)

           А В С = (А В) С = А (В С)

     3) если АÌВ, то А В=В;