Министерство образования Российской Федерации
Новосибирский государственный технический университет
С.В. Ренин
Сборник задач и упражнений для студентов
II курса дневного отделения и III курса заочного
отделения АВТФ (специальность 22.02)
Новосибирск
2000
Ренин С.В. Спецглавы математики. Сборник задач и упражнений / Новосиб. гос. технич. ун-т. – Новосибирск, 2000. –
Сборник содержит задачи и упражнения по основным разделам курса «Спецглавы математики» и предназначается студентам специальности «Автоматизированные системы обработки информации и управления» АВТФ НГТУ для использования при подготовке к практическим занятиям и при самостоятельной работе над курсом.
Может быть рекомендован также студентам других специальностей, изучающим аналогичные курсы, в частности, студентам Института социальной реабилитации НГТУ.
Рецензент: к. т. н., доцент В.С. Поздняков
(С) Новосибирский государственный технический университет
Курс «Спецглавы математики» призван дать студентам подготовку в области математических методов, лежащих в основе анализа и синтеза сложных систем управления. В результате изучения курса студенты должны, в частности, овладеть основными понятиями и методами теории множеств, теории графов и комбинаторного анализа, а также получить твердые навыки решения задач, относящихся к указанным разделам математики.
Настоящий сборник задач и упражнений содержит материал, необходимый для подготовки и выполнения практических занятий по курсу «Спецглавы математики», а также для использования студентами при самостоятельной работе над курсом. Известные автору задачники и другие пособия по перечисленным разделам математики [1-3] уже стали библиографической редкостью, кроме того, они не соответствуют в полной мере программе названного курса, утвержденной для специальности 22.02, и характеризуются значительными расхождениями в терминологии, что затрудняет их использование.
Весь материал сборника разбит на разделы в соответствии с темами практических занятий, предусмотренными программой курса. В начале каждого раздела даны основные понятия и определения, необходимые для решения задач, или ссылки на доступные студентам пособия [4-6]. Приведены также примеры и методические указания по решению типовых задач. Завершается каждый раздел задачами и упражнениями для самостоятельной работы. Задачи и упражнения нумеруются двумя цифрами, первая из которых совпадает с номером раздела, а вторая служит порядковым номером внутри раздела. В конце приведены ответы и указания к решению некоторых задач.
1. МНОЖЕСТВА. ОТНОШЕНИЯ НА МНОЖЕСТВАХ
Для решения задач, предлагаемых в данном разделе, необходимо проработать теоретический материал [4, с. 5-15, или 5, с. 7-44, или 6, с. 24-66].
В задачах множества обозначаются прописными буквами латинского алфавита (с индексами или без них); элементы множеств – строчными буквами латинского алфавита (с индексами или без них); I – универсальное множество;
![]() – разность множеств А и В;
– разность множеств А и В;
![]() – дополнение
множества А (до универсального множества);
– дополнение
множества А (до универсального множества);
(а1, а2,…,аn) – упорядоченное множество (кортеж, n-ка);
А1´A2´…´An = {(а1, а2,…,аn)|
ai ÎAi, i = ![]() }- декартово (прямое) произведение
множеств А1, A2,…, An.
}- декартово (прямое) произведение
множеств А1, A2,…, An.
Для сокращения записи в тексте используются следующие логические символы:
Ù - связка “и”;
Ú - связка “или”;
Þ - если … то (логическое следование);
Û - тогда и только тогда, когда (эквивалентно);
"x P(x) – для всех х высказывание P(x) истинно;
$ x P(x) – существует такое х, что высказывание P(x) истинно.
Ниже приведены основные понятия и определения, необходимые для решения задач.
Соответствие есть тройка множеств q = (X, Y, Q), где Q Í X ´Y , X – область отправления, Y – область прибытия, Q – график соответствия.
Пр1 Q – множество первых элементов пар (х, у) Î Q (область определения соответствия);
Пр2 Q – множество вторых элементов пар (х, у) Î Q (область значений соответствия).
M(Q) = ||qij|| - матрица соответствия,
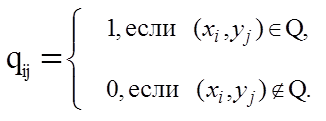
q-1 = (Y, X, Q-1), Q-1 Í Y´X – соответствие, обратное соответствию q;
Q-1 = {(y, x)| (x, y) Î Q}.
q○p = (X, Z, Q○P), Q○P Í X´Z – композиция соответствий q = (X,
Y, Q),
Q Í X´Y,
и p = (Y, Z, P), P Í Y´Z, причем
(x, z) Î Q○P Û $yÎY ((x, y) Î Q Ù (y, z) Î P).
Соответствие (X, Y, G), G Í X´Y, называется отображением Х в Y, если Пр1Г = Х; если при этом Пр2 = Y, то Г – отображение Х на Y.
Гх = {y| (x, y) Î Г} – образ элемента xÎX в отображении Г.
Г-1y = {x| (x, y) Î Г} – прообраз элемента yÎY в отображении Г.
|X| – количество элементов множества Х.
Отображение (X, Y, f), f Í X´Y, называется функцией, если
"xÎX (|Гх| = 1).
Отношение (бинарное) на множестве Х есть пара (X, R), где R Í X´Х. Если Х задано, то вместо (X, R) пишут просто R. Запись xRy означает, что элемент “х” находится в отношении R к элементу “y”, т.е. (x, y) Î R.
Транзитивным замыканием отношения R
называется пара ![]() , где
, где ![]() причем
причем ![]() существует цепочка элементов z0 =
x, z1, z2, … ,
существует цепочка элементов z0 =
x, z1, z2, … ,
zn = y), такая, что каждый предыдущий элемент цепочки находится в
отношении R со следующим элементом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.