Математика \ Специальные главы математики

Спецглавы математики: Сборник задач и упражнений, страница 2

Основные свойства, которыми могут обладать отношения:

рефлексивность - "хÎХ (xRx);

антирефлексивность - "х"y (xRy Þ x ¹ y);

симметричность - "х"y (xRy Þ yRx);

асимметричность - "х"y ((x, y)Î R Þ (y, x) Ï R);

антисимметричность - "х"y (xRy Ù yRx Þ y = x);

транзитивность - "х"y"z (xRy Ù yRz Þ xRz).

Отношение R есть отношение эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно. Отношение R есть отношение (нестрогого) частичного порядка, если оно рефлексивно, антисимметрично и транзитивно. Отношение R есть отношение строгого частичного порядка, если оно асимметрично и транзитивно.

Для решения большинства предлагаемых задач достаточно знать определения и правила выполнения операций, изложенные в работах [5, 6]. Для нахождения композиции соответствий (X, Y, R) и (Y, Z, S), заданных с помощью матриц, можно воспользоваться тем, что матрица композиции M(Q) = M(R○S) может быть получена как булево произведение матриц M(R) и M(S), элементы которого определяются по формуле

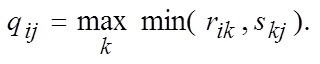
Пример 1.1. Для соответствий (X, Y, R), где R = {(x1, y1), (x1, y2), (x2, y3), (x2, y4)}, и (Y, Z, S), где S = {(y1, z1), (y2, z1), (y3,z2), (y4, z2)}, дать их графическое и матричное представления и найти композицию соответствий.

Решение.

                           Y

у1
 
Х                                                   Z                           X                             Z

                                                                                                                  

у2
 
                           

у3
 
                           

                                                                                                                  

у4
 
                           

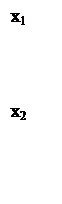
            R                           S                                                  Q = R○S

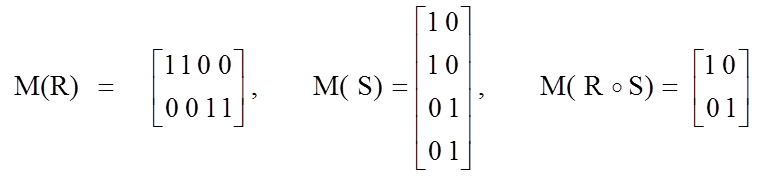
Пример 2. Найти транзитивное замыкание отношения (A, R), если
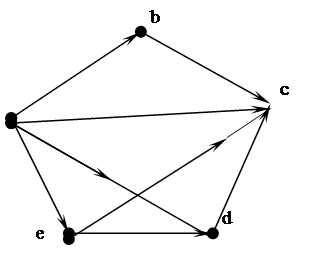
A = {a, b, c, d, e}, R = {(a, b), (b, c), (d, c), (e, d), (a, e)}.

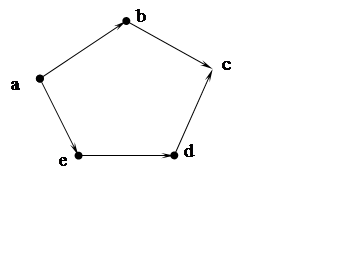
Решение. Для нахождения транзитивного замыкания отношения удобно это отношение представить в графической форме. Как следует из определения этой операции, , т.е. все элементы графического представления отношения R входят в графическое представление отношения  . Кроме того, если в графическом представлении отношения R имеются последовательности стрелок (пути), в которых конец предыдущей стрелки совпадает с началом последующей, то необходимо добавить стрелки, направленные от начала такого пути к его концу.

 


   R                                                            

a

 
 


Задачу можно решить и аналитически. Для этого воспользуемся соотношением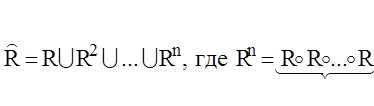. Переходя к матрице, получим

В последней формуле при вычислении матрицы композиции отношений применяется булево произведение матриц, а объединение матриц отношений M(Q) = ||qij|| и M(S) = ||sij||, заданных на одном и том же множестве, производится по формуле

tij = max (qij, sij),                                           (1.2)

Максимальная степень, в которую нужно возвести матрицу M(R) в выражении (1.1), не превосходит числа элементов множества А.

В рассматриваемом примере

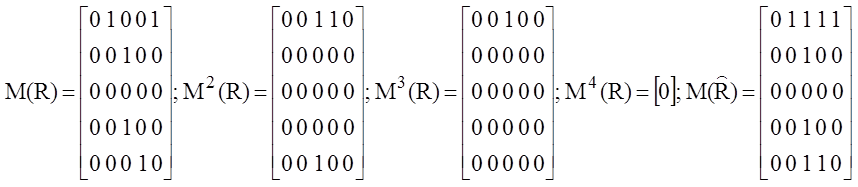
Нетрудно видеть, что последняя матрица полностью соответствует графическому представлению отношения

Задачи

1.1.  Перечислите все элементы и все подмножества множества {1, 2, {3, 4}}.

1.2.  Множество букв русского алфавита обозначили буквой С. Укажите среди следующих высказываний истинные:
а) б Î С; б) ю Î С; в) z Ï С; г) t Î C; д) 33Î С.

1.3.  Укажите, какие из следующих утверждений справедливы:

Скачать файл