б) Х –
множество деталей; Y – множество технологических операций;
Z – множество рабочих; R = {(x, y)| над деталью х выполняется операция у};
S = {(y, z)| операцию у выполняет рабочий z};
в) Х – множество преподавателей университета; Y – множество читаемых дисциплин; Z – множество учебных групп; R = {(x, y)| преподаватель х ведет занятия по дисциплине у}; S = {(y, z)| дисциплина у преподается студентам группы z};
г) Х – множество мужчин; Y – множество людей; Z – множество женщин; R = {(x, y)| х – отец у}; S = {(y, z)| y – родитель z}?
Что означает для этих примеров соответствие (R○S)–1?
1.21. X = {x1,
x2, x3, x4}, Y = {y1, y2,
y3, y4}, Z = (z1, z2, z3),
R = (x1, y2), (x2, y1),
(x3, y1), (x3, y3); S = {(y1,
z1), (y1, z2), (y2, z1),
(y3, z3), (y4, z1)}.
Матричным и графическим способом найдите соответствия R○S, (R○S)–1, S–1○ R–1.
1.22. Для следующих соответствий найдите область определения, область значений и определите тип соответствия; сделайте то же самое для соответствий, обратных заданным.
а) (N, Y, R), R Í N ´ Y; Y – множество многочленов; N – множество натуральных чисел; R = {(n, y)| n – степень многочлена у};
б) (С, E, R), C – множество комплексных чисел; Е – множество действительных чисел; R = {(х, у)| x Î C; y Î E; модуль х равен у};
в) (Х ´Y, Z, S), S Í
(Х ´Y) ´
Z; X – множество прямых на плоскости, параллельных заданной прямой a; Y – множество прямых на той же плоскости,
не параллельных a; Z – множество точек
этой плоскости;
S = {((x, y), z)| прямая х Î Х
пересекается с прямой у Î Y в точке
z Î Z}.
1.23. Назовите известные вам отношения на следующих множествах:
а) множество натуральных чисел;
б) множество треугольников;
в) множество государств;
г) множество морей;
д) множество людей;
е) множество уравнений.
Какими свойствами обладают эти отношения, к какому виду относятся?
1.24. Найдите область определения и область значений для отношений «быть отцом» и «быть братом» на множестве людей.
1.25. Запишите график
R следующих отношений, заданных на множестве
Х = {0, 2, 4, 6, 8, 9}. Дайте их графическое и матричное представление, найдите
область определения и область значений.
а) x <
y; б) х делится на у; в) х в 2 раза больше у;
г) х на 2 больше у;
д) х £ у; е) х –
делитель у; ж) х + у = 6.
1.26. Дайте
графическое и матричное представление отношения (X, R), где
Х = {a, b, c, d, e, f}, R = {(a, a), (a, c), (a, f), (b, a), (b, e), (d, a),
(d, d), (d, f), (f, b), (f, c), (f, e), (e, f)}.
1.27. Представьте в матричной форме следующие отношения, заданные графически, запишите график этих отношений.
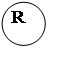 |
 |
 |
|
|
|
|
|
|
|
|
|
|





 |
|||||||||
![]()
![]()
1.28. Отношения R и S
заданы на множестве людей:
R = {(x, y)| x – брат у}, S = {(x, y)| x – жена у}.
Что означают отношения R○S и S○R?
1.29. Для отношений R, S и T, представленных в упражнении 1.27, найти:
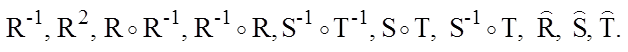
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.