Спецглавы математики: Сборник задач и упражнений, страница 9

Пример 3.1. Сколько существует четырехзначных чисел, больших или равных 1000, в которых цифра 3 встречается ровно 1 раз?

Решение. Четырехзначные числа можно рассматривать как расстановки из элементов 10 типов (цифр 0, 1, 2, …, 9) по 4, причем порядок следования элементов имеет значение, и все цифры, кроме цифры 3, могут встречаться несколько раз.

Так как цифра 3 в каждой расстановке может встречаться только один раз и занимает при этом  ровно одно из четырех возможных мест, то все множество расстановок можно разбить на 4 непересекающихся подмножества (в расстановках из i-го подмножества цифра 3 занимает i-ое место слева).Пусть цифра 3 стоит на первом месте слева, тогда остальные разряды могут быть заполнены любыми из оставшихся 9 цифр, т.е. могут рассматриваться как размещения с повторениями из элементов 9 типов по 3. По формуле (3.4) число таких размещений равно 9³ = 729.

Пусть теперь цифра 3 стоит на втором, третьем или четвертом месте слева. Из трех свободных мест первое слева может быть заполнено любой из оставшихся 9 цифр, кроме 0, т.е. существует 8 способов заполнения этого места. На каждое из следующих двух мест можно поставить любую из 9 цифр. Так как количество вариантов заполнения каждого из этих разрядов не зависит от того, как были заполнены остальные разряды, то можно воспользоваться  правилом произведения: число расстановок в каждом из этих подмножеств равно

8 × 9 × 9 = 648.

По правилу суммы общее число рассматриваемых расстановок равно

729 + 3 × 648 = 2673.

Пример 3.2. Сколькими способами можно расставить белые фигуры (2 коня, 2 слона, 2 ладьи, ферзя и короля) на первой линии шахматной доски?

Решение. Поскольку порядок следования элементов имеет значение и каждая расстановка включает в себя все 8 элементов пяти типов, причем некоторые элементы повторяются, то эти расстановки являются перестановками с повторениями из элементов 5 типов. Их количество определим по формуле (3.5):

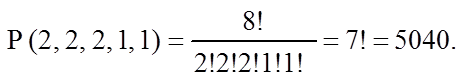
Задачи

3.1.  Сколько элементов содержит декартово произведение А ´ В ´ С, если
|A| = 12, |B| = 5, |C| = 8?

3.2.  Из города А в город В ведут 5 дорог, из В в С – 3 дороги. Сколько дорог ведут их А в С через В?

3.3.  Имеется 5 видов конвертов без марок и 4 вида марок одного достоинства. Сколько существует способов выбора конверта с маркой?

3.4.  На вершину горы ведут 5 дорог. Сколькими способами турист может подняться на гору и спуститься с нее? То же, если подъем и спуск должны идти разными путями?

3.5.  Сколькими способами можно указать на шахматной доске два квадрата – белый и черный? То же, если нет ограничений на цвет квадратов?

3.6.  Сколькими способами можно указать на шахматной доске белый и черный квадраты, если они не должны лежать на одной и той же вертикали и горизонтали?

3.7.  В букинистическом магазине лежат 6 экземпляров романа И.С. Тургенева «Рудин», 3 экземпляра романа «Дворянское гнездо», 4 экземпляра романа «Отцы и дети», 5 томов, содержащих романы «Рудин» и «Дворянское гнездо», 7 томов с романами «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из романов?

3.8.  У некоторых народов принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более 3 имен?

3.9.  В профсоюзный комитет выбрано 9 человек. Из них нужно избрать председателя, заместителя, секретаря и спортивного организатора. Сколькими способами можно это сделать? То же, если должностей 9?

3.10.  4 студента сдают  экзамен. Сколькими способами им могут быть поставлены оценки, если никто из них не получил неудовлетворительной оценки?

3.11.  В селении проживают 2000 жителей. Доказать, что по крайней мере двое из них имеют одинаковые инициалы.

3.12.  На полке находятся  m+n различных книг, из которых m книг имеют черные переплеты, а n книг – красные. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают m первых мест? Сколько существует положений, когда все книги в черных переплетах стоят рядом?