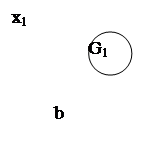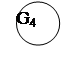Спецглавы математики: Сборник задач и упражнений, страница 7

х2

·

·

а)                            б)                            в)                              г)

		d

 

х3

х4

х5

х2

·

·

·

·

·

·

·

·

·

·

д)                            е)                            ж)                              з)

 

2.2. Дайте графическое и матричное представление следующих графов:

а)   G₁ = (X₁, Г₁), где Х₁ = {х₁, х₂, х₃, х₄, х₅}, Х₁/Г₁ = {Г₁х₁ = {х₃, х₄, х₅}; Г₁х₂ = Æ; Г₁х₃ = {х₃}; Г₁х₄ = {х₁, х₅}; Г₁х₅ = {х₂}};

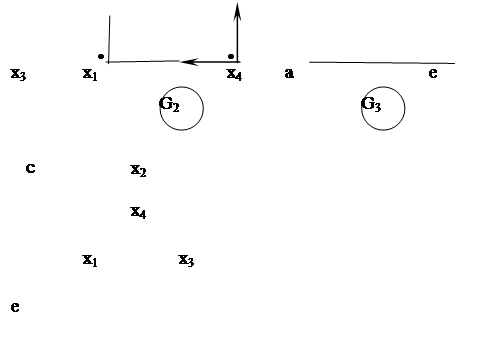
б)   G₂ = (X₂, Г₂), где Х₂ = {х₁, х₃, х₆}; Х₂/Г₂ = {Г₂х₁ = {х₆}; Г₂х₃ = Х₂; Г₂х₆ = {х₁, х₃}};

в)   G₃ = (Х₃, Г₃), где Х₃ = Х₂ (см. пункт б); Х₃/ Г₃ = {Г₃х₁ = {х₁, х₃}; Г₃х₃ = Æ; Г₃х₆ = {х₃}};

г)   G₄ = (Х₄, Г₄), где Х₄ = {х₁, х₂, х₃, х₄}, Х₄/Г₄ = {Г₄х₁ = {х₂, х₃}; Г₄х₂ = {х₁, х₃}; Г₄х₃ = {х₁, х₂}; Г₄х₄ = Æ};

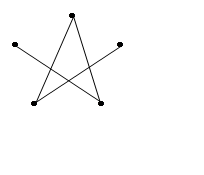
д)   G₅ = (Х₅, Г₅), где Х₅ = Х₄ (см. пункт г); Х₅/Г₅ = {Г₅х₁ = {х₃, х₄}; Г₅х₂ = Æ;
Г₅х₃ = {х₁, х₄}; Г₅х₄ = {х₁, х₃}}.

2.3. Дайте аналитическое и графическое представление следующих графов, заданных матрицами смежности:

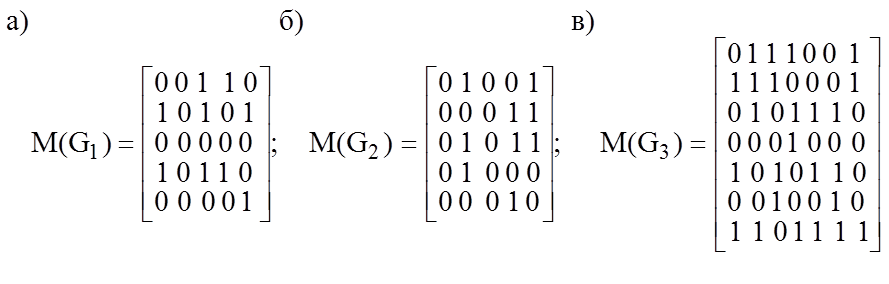
2.4. Какие из графов, представленных в упражнениях 2.1 – 2.3, являются ориентированными, неориентированными, смешанными?

2.5. Приведите примеры частичных графов, используя в качестве исходных графы G₆, G₇ и G₈ из упражнения 2.1.

2.6. Постройте подграфы графа G₈ из упражнения 2.1, определяемые соответственно множествами {х₁, х₂, х₅} и {х₁, х₂, х₄, х₅}. Приведите примеры частичных подграфов графа G₈, определяемых теми же множествами.

2.7. Выполните следующие операции над графами из упражнения 2.1:

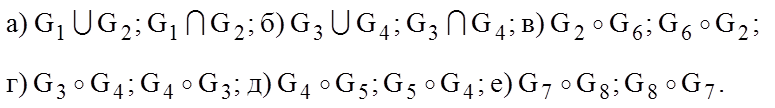
2.8. Выполните следующие операции над графами из упражнения 2.2:

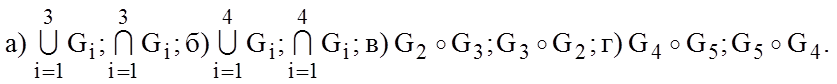
Дайте графическое представление полученных результатов.

2.9. Выполните следующие операции над графами из упражнения 2.3, полагая, что графы, над которыми выполняется операция, заданы на одном и том же множестве вершин:

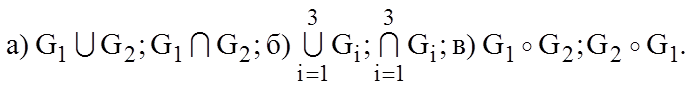
2.10. Найти транзитивное замыкание графов из упражнения 2.1.

2.11. Найти транзитивное замыкание графов, построенных в упражнениях 2.8, 2.9.

2.12. Используя графы G₆, G₇ и G₈ из упражнения 2.1, привести примеры элементарных, простых и составных путей, цепей, контуров и циклов. Указать их длины.

2.13. Связны ли следующие неографы, заданные своими матрицами смежности? Если нет, то сколько в них связных компонент?

2.14.  Являются ли следующие графы связными? Если нет, то разложите их на максимальные сильно связные подграфы.

2.15.  В следующих графах найти минимальный каркас:

                                  

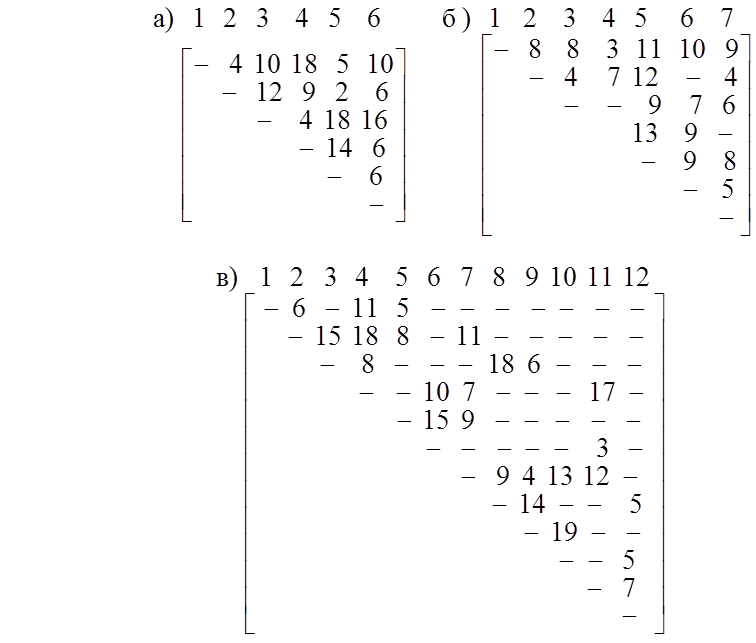
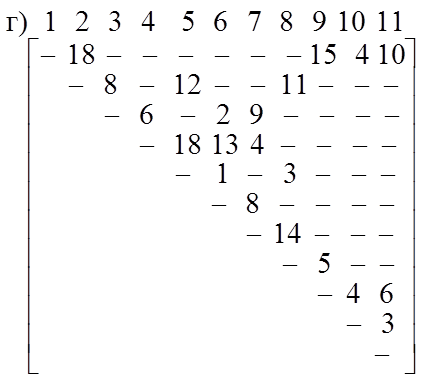
2.16.  В графах из упражнения 2.15 найти кратчайшие цепи, соединяющие вершину х₁ со всеми остальными вершинами.

2.17.  В следующих графах найти кратчайшие пути из вершины х₁ во все остальные вершины.

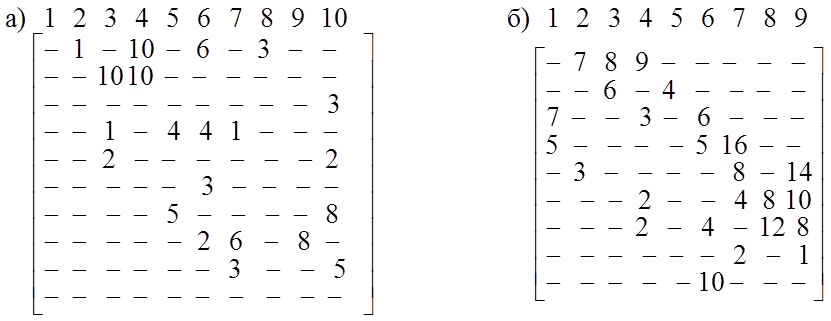
2.18.  В следующих графах найти длиннейший путь:

а) из х₀ в х₁₁ 

   

б)  из х₀ в х₁₂

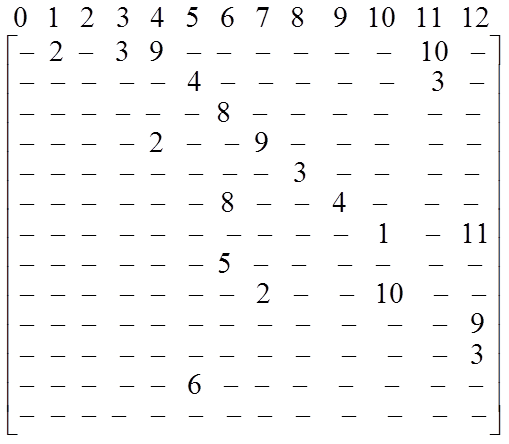
в)  из х₁ во все остальные вершины

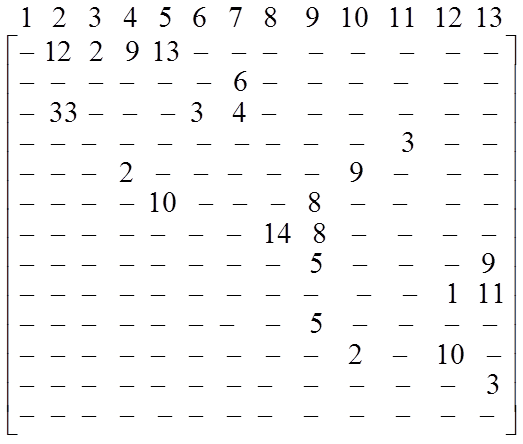
3.  КОМБИНАТОРИКА