Математика \ Специальные главы математики

Спецглавы математики: Сборник задач и упражнений, страница 3

а) {Æ} = Æ;

д) {1, 2} Í {{1, 2, 3}, {1, 3}, 1, 2};

б) {0} = Æ;

е) {3} Î {1, 2, 3, 4};

в) {{1, 2}, {2, 3}} ¹ {1, 2, 3}

ж) 3 Î {1, 2, 3, 4};

г) {1, 2} Î {{1, 2, 3}, {1, 3}, 1, 2};

з) 3 Î {1, 2, {3}, 4}.

          Верно ли, что:
а) х Î А; б) х Î В; в) х Ï А; г) х Ï В; д) х Î А и х Î В; е) х Î А и х Ï В.

1.5.

Можно ли на основании этого утверждать, что:
а) х Î А; б) х Î В; в) х Ï А; г) х Ï В; д) х Î А или х Î В; е) х Î А и х Î В.

1.6.    Упростите следующие выражения, если А Í В:

1.7.  А – множество прямоугольников, В – множество квадратов. Установите, в каком отношении находятся данные множества, изобразите их при помощи диаграмм Эйлера-Венна и среди следующих высказываний укажите истинные:
 

1.8.  Запишите результаты объединения, пересечения и вычитания множеств А и В (для вычитания – А\В и В\А), если:
а) А = {k, l, f, t, u},   B = {k, l, m, n, o, p};
б) A = {6, 3, 2, 5, 13},  B = {13, 3, 2, 5, 6};
в) A = {5, 10, 15, 20, 25, 30}, B = {10, 20, 30}.

1.9.  Используя свойства операций над множествами, упростите выражения:

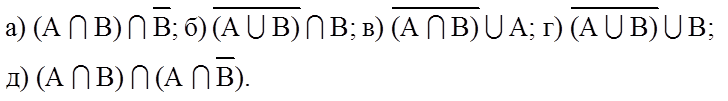
1.10.  Телестудия провела опрос группы телезрителей, чтобы выяснить их реакцию на одну из передач. Результаты опроса приведены в таблице.

Категория

зрителей

Реакция на передачу

Очень понравилась

Понравилась, но не очень

Не понравилась, но не очень

Очень не понравилась

Мужчины

Женщины

Мальчики

Девочки

1

6

5

8

3

8

5

5

5

3

3

1

10

1

2

1

Обозначим: М – множество зрителей мужского пола; В – множество взрослых телезрителей; П – множество телезрителей, которым передача понравилась;
О – множество телезрителей, которым передача очень понравилась или очень не понравилась.

Сколько человек входит в каждое из множеств:

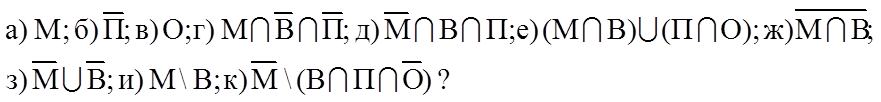
1.11.  Обозначим: Z – множество целых чисел; Q – множество рациональных чисел; Е – множество вещественных чисел. Что представляют собой следующие множества:

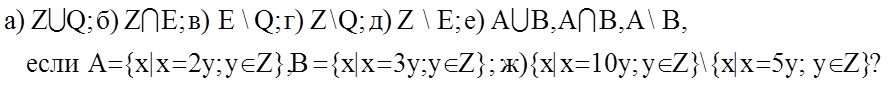
1.12.    Обозначим: N – множество натуральных чисел; Е – множество вещественных чисел. Изобразите на координатной плоскости элементы множества Х ´ Y, если:
а) X = {x | x Î N, x = 3},  Y = {y | y Î R, 3 £ y £ 6};
б) X = {x | x Î R, -1 £ x £ 3}, Y = {y | y Î N, y = 3};
в) X = {x | x Î N, x £ 3}, Y = {y | y Î R, 3 £ y £ 6};
г) X = {x | x Î R, -1 £ x £ 3}, Y = {y | y Î N, y £ 3}.

1.13.  Доказать, что в общем случае:
а) А ´ В  ¹ В ´ А;  в)  А ´ (В ´ С) ¹ (А ´ В) ´ С.

1.14.  Дать геометрическую интерпретацию множеств:
 а) [a, b] ´ [c, d], где [a, b], [c, d] – отрезки действительной прямой;
 

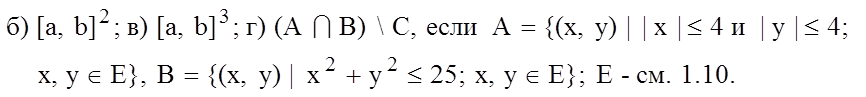
1.15. Упростите выражения:

1.16.  Упростите выражения:

 

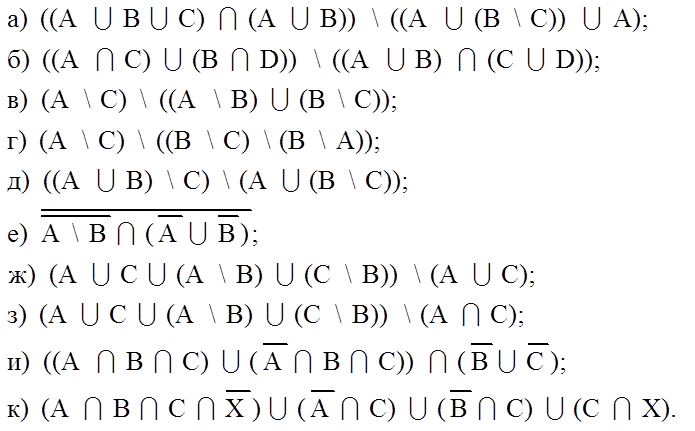
1.17. Приведите известные вам соответствия между элементами следующих  
         множеств:

а) множество людей и множество городов;

б) множество студентов и множество преподавателей;

в) множество треугольников и множество целых чисел;

г) множество треугольников и множество окружностей;

д) множество многоугольников и множество натуральных чисел;

Укажите, к какому типу относятся эти соответствия.

1.18. Представьте графически и в виде матрицы соответствие (X, Y, Q), если:
а) X = {2, 4, 6}, Y = {1, 3, 5}, Q = {(x, y)| xÎX; yÎY; x > y};
б) X = {25, 16, 7, 6}, Y = {2, 5, 3, 9, 1}, Q = {(x, y)| xÎX; yÎY;
    x делится на y};
в) X = {ромб, круг, куб, угол}, Y = {о, у, л, г, б, к, р, м}; Q = {(x, y)| xÎX;
            yÎY; в слово х входит буква у};
г) X = {x1, x2, x3, x4}, Y = { y1, y2, y3, y4},
            Q = {(x1, y4), (x2, y2), (x3, y3), (x4, y1)};

Постройте соответствия, обратные данным.

1.19.  Обратно ли соответствие «х – брат у» соответствию «у – сестра х», если:
а) X = Y – множество всех людей;
б) Х – множество мужчин; Y – множество женщин?

1.20.  Что означает композиция соответствий (X, Y, R) и (Y, Z, S), если:

а) Х – множество точек плоскости; Y – множество окружностей; Z – множество треугольников, R = {(x, y)| точка х – центр окружности у};
S = {(y, z)| окружность у вписана в треугольник z};

Скачать файл