Спецглавы математики: Сборник задач и упражнений, страница 6

Решение. Для отыскания максимальных сильно связных подграфов воспользуемся алгоритмом  Мальгранжа. Выберем произвольную вершину, например, х₁ и, используя M(G), найдем множество вершин, достижимых из х₁ по как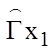ому-либо пути (), и множество вершин, из которых можно попасть в х₁ по какому-либо пути (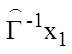). Элементы первого множества выделим цифрами в дополнительном столбце справа от матрицы смежности, а элементы второго множества – в дополнительной строке под матрицей. Цифры означают расстояние от х₁ до х_i в первом случае и от x_i до х₁ – во втором. Вершины, не достижимые из х₁ в графе G (или G^-1) отметим в дополнительном столбце (строке) крестиками.

Множество вершин максимального сильно связного подграфа, содержащего вершину х₁,

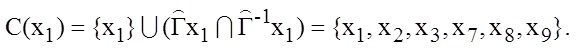
Вычеркнем из матрицы M(G) строки и столбцы, соответствующие элементам множества С(х). В результате получим матрицу М₁, определяющую некоторый подграф графа G:

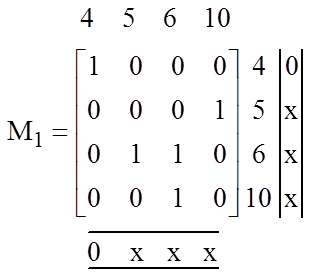
В полученном подграфе выберем произвольную вершину (например, х₄) и произведем операции, аналогичные описанным выше. В результате получим:

С(х₄) = {x₄}.

Вычеркнем из М₁ строку и столбец, соответствующие вершине х₄; получим матрицу:

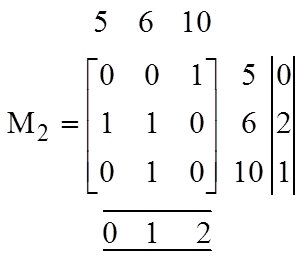
Выберем в оставшемся подграфе вершину х₅. Нетрудно убедиться, что С(х₅) включает в себя все вершины этого подграфа, т.е.

С(х₅) = { х₅, x₆, x₁₀}.

Таким образом, рассматриваемый граф включает в себя три максимальных сильно связных подграфа, определяемых множествами вершин С(х₁), С(х₄) и С(х₅), и, следовательно, не является сильно связным. Матрицы смежности этих подграфов имеют вид:

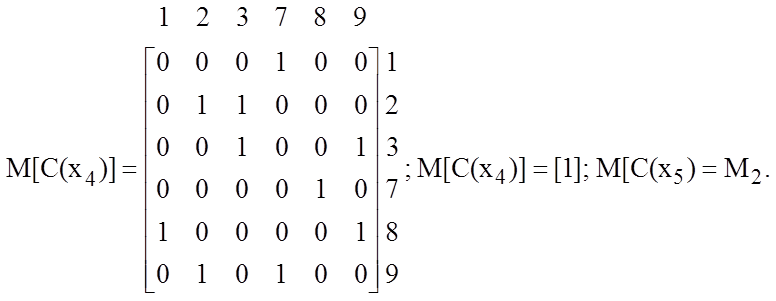
Для решения вопроса о связности графа G построим матрицу смежности соотнесенного неографа G_u:

 

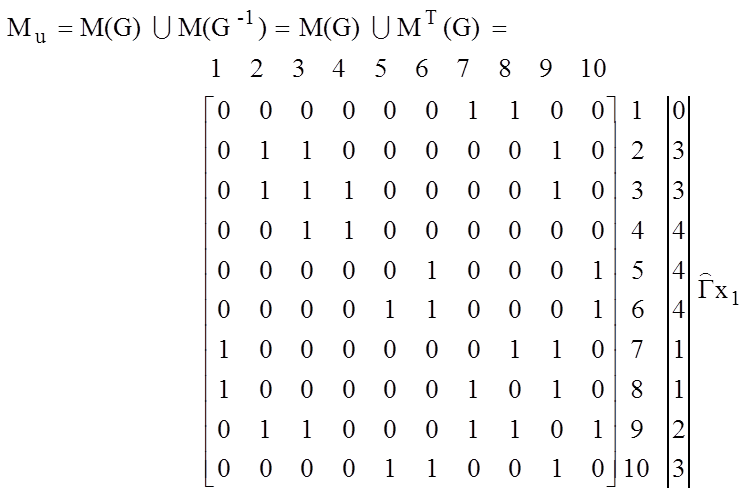
Индекс Т над обозначением матрицы означает транспонирование.

Используя матрицу M_u, найдем множество вершин, достижимых из произвольной вершины x_i соотнесенного неографа (). В данном случае оказалось, что , следовательно, графы G_u и G являются связными.

После разбора этого примера постройте самостоятельно чертежи всех максимальных сильно связных подграфов и графа G в целом.

Пример 2.2. В неографе G = (X, Г), заданном матрицей мер М_m(G), построить минимальный каркас (экономическое дерево). Здесь и в дальнейшем знак
“-” в матрице смежности означает отсутствие ребра.

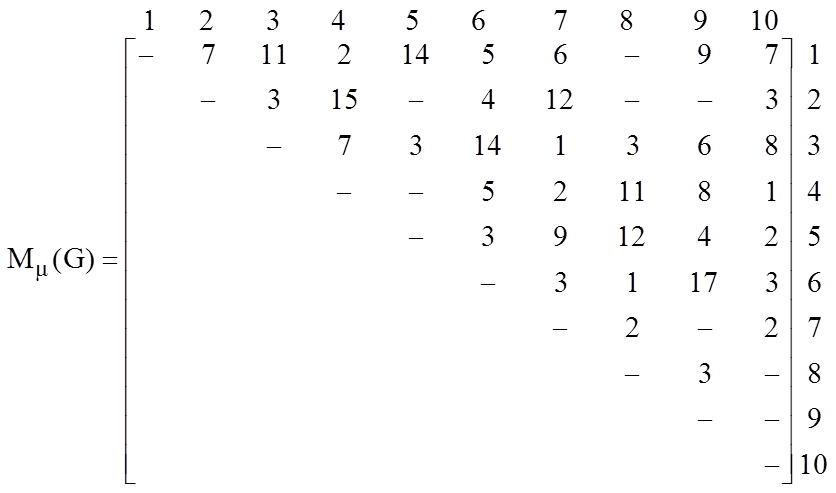
Решение. Известно [4], что для существования в графе каркаса, т.е. частичного графа, являющегося деревом, необходимо и достаточно, чтобы граф был связным. Проверку связности можно произвести с помощью алгоритма Мальгранжа (см. предыдущий пример). Выполните это самостоятельно.

Построение минимального каркаса осуществляется за n-1 шаг, где n – количество вершин графа. В нашем случае число шагов равно 9. На каждом шаге из множества неиспользованных ребер выбирается одно, имеющее минимальную меру, если только его добавление к частичному подграфу, составленному из уже выбранных ребер, не приведет к образованию цикла. В противном случае выбирается другое ребро  с минимально возможной мерой. В нашей задаче ребра могут быть выбраны, например,  в такой последовательности:

(х₃, х₇), (х₄, х₁₀), (х₆, х₈), (х₁, х₄), (х₄, х₇), (х₅, х₁₀), (х₇, х₈), (х₂, х₃), (х₈, х₉)

     ^{1                   1                     1                 2                  2                    2                    2                    3                  3}

Цифры под обозначениями ребер означают их длину.

Если число вершин графа не слишком велико, то построение минимального каркаса целесообразно сопровождать чертежом, что облегчает выявление циклов при добавлении новых ребер.

В данном графе можно построить несколько различных минимальных каркасов (имеющих, естественно, одну и ту же суммарную меру).

Задачи

d

2.1. Дайте аналитическое и матричное представление следующих графов:

	х2		х3		b		c