3.13. У одного человека есть 7 книг по математике, а у другого – 9 других книг. Сколькими способами они могут произвести обмен, если 2 книги одного меняются на 2 книги другого?
3.14. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить 12 открыток? 8 открыток? 8 различных открыток?
3.15. Секретный замок с шифром имеет 5 дисков с 12 буквами на каждом. Какое максимальное количество времени может потребоваться человеку, не знающему секретного слова, чтобы открыть замок, если на каждую попытку он тратит 6 секунд?
3.16. Найти число способов расстановки 8 ладей на шахматной доске, чтобы они не били друг друга.
3.17. В магазине продается 4 сорта пирожных. Сколькими способами можно купить 7 пирожных?
3.18. Каким количеством способов можно заполнить карточки «Спортлото» 6 из 49?
3.19.
В «Спортлото» 6 из 49 играют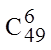 
человек. Все они
заполнили карточки по-разному. Сколько человек угадают 6, 5, 4, 3, 2 и 1 номер?
3.20. Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если: а) ни одна из цифр не встречается более одного раза; б) цифры могут повторяться; в) числа должны быть нечетными (цифры могут повторяться)?
3.21. Из города А в город В ведет k дорог, а в город С – s дорог. В город D из города В ведет m дорог, а из города С – n дорог. Города В и С дорогами не соединяются. Сколько различных автобусных маршрутов можно провести между городами А и D?
3.22. В осеннем семестре студентам читаю лекции по 8 дисциплинам. Сколькими способами можно составить расписание на понедельник, если в этот день должны читаться 3 лекции?
3.23. Дано n точек, никакие три из которых не лежат на одной прямой. Сколько прямых можно провести, соединяя эти точки попарно?
3.24.
На плоскости проведено n прямых так, что никакие две из них не параллельны
и никакие три не пересекаются в одной точке. Найти количество точек пересечения
этих прямых и определить, сколько треугольников образуют эти прямые?
ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
1.3. в, д, ж; 1.4. а) 34; б) 26; в) 34; г) 5; д) 14; е) 38; ж) 48; з) 48; и) 15; к) 25;
1.16. а) В\А; б) Æ; г) (А\В)\С; 3.1. 480; 3.2. 15; 3.3 20;
3.4. 25; 20; 3.5. 1024; 2016; 3.6. 768; 3.7. 134; 3.8. 26820600; 3.9. 3024; 9!;
3.10. 81; 3.11. Покажите, что число возможных инициалов меньше числа жителей.
3.12. m!n!; m!(n+1)! 3.13. 756; 3.15. около 415 часов; 3.16. 40320; 3.17. 120;
3.18. 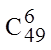; 3.20. а) 300; б) 1080;
в) 540; 3.21. km + sn; 3.23. n(n-1)/2; 3.24.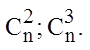 
Литература
1. Гаврилов Г.П., Сапоженко А.Л. Сборник задач по дискретной математике. – М.: Наука, 1977. – 368 с.
2. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука, 1975. – 240 с.
3. Бельский А.А., Липкина З.С. Математическая логика и теория графов. – М.: МИИТ, 1974. – 34 с.
4. Основы кибернетики. Математические основы кибернетики / Под ред. К.А. Пупкова. – М.: Высшая школа, 1974. – 413 с.
5. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергия, 1980. – 424 с.
6. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987. – 496 с.
7. Виленкин Н.Я. Комбинаторика. – М.: Наука, 1969. – 328 с.
8. Кофман
А. Введение в прикладную комбинаторику. – М.: Наука, 1975.
– 480 с.
9. Кристофидес Н. Теория графов. – М.: Мир, 1978. – 432 с.
10. Белов В.А., Воробьев Е.Н., Шаталов В.Е. Теория графов. – М.: Высшая школа, 1976. – 392 с.
11. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988. – 480 с.
12. Сборник задач по математике: А.М. Пышкало, Л.П. Стойлова, Н.Н. Лаврова, Н.П. Ирошников. – М.: Просвещение, 1979. – 208 с.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ ……………………………………………………………………….. 3
1. Множества. Отношения на множествах ……………………………………... 3
2. Теория графов …………………………………………………………………. 12
3. Комбинаторика ……………………………………………………………….. 22
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.