М[С(х4)]=[1].
Вычеркнем из М1 строку и столбец, соответствующие вершине х4; получим матрицу М2, с которой выполним описанные выше операции, выбрав для этого вершину х5:
![]()
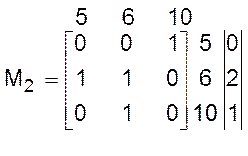
![]() 0 1 2
0 1 2
Нетрудно видеть, что из вершины х5 можно попасть в любую из оставшихся вершин и вернуться обратно, т.е. подграф, определяемый матрицей М2, сильно связен, C(х5) = {х5, х6, x10} и М[C(х5)] = М2.
Итак, граф G имеет три максимальных сильно связных подграфа, определяемых матрицами M[C(x1)], М[С(х4)] и М[C(х5)].
Упражнение. Дайте графическое изображение графа G и всех трех найденных подграфов, сопоставьте эти изображения между собой. Чем отличается исходный граф G от объединения его максимальных сильно связных подграфов?
2.5. Деревья
2.5.1. Определение и свойства деревьев
Деревом называется конечный связный неограф без циклов (в том числе без петель и кратных ребер), имеющий не менее двух вершин.
Лесом называется граф без циклов, все связные компоненты которого являются деревьями.
Дерево, построенное на n вершинах, обладает следующими свойствами:
1) оно содержит n -1 ребро;
2) добавление к дереву любого ребра между существующими вершинами приводит к образованию цикла;
3) удаление из дерева любого ребра приводит к потере связности;
4) любые две вершины дерева связаны между собой цепью и притом только одной.
Пусть G(X) - произвольный связный неограф. Можно доказать, что такой граф всегда содержит в себе частичный граф, являющийся деревом. Такое дерево называется покрывающим деревом или каркасом графа G(X).
2.5.2. Задача о минимальном каркасе
Пусть G(X) – связный неограф с нагруженными ребрами (т.е. с ребрами, которым поставлены в соответствие некоторые меры). Необходимо построить каркас этого графа Т(Х), такой, чтобы сумма мер, приписанных его ребрам, была минимально возможной.
Такая задача называется задачей о минимальном каркасе.
Эта задача имеет наглядную содержательную интерпретацию: если граф G(X) описывает сеть дорог, которые можно построить между городами, представляемыми множеством вершин Х, и мера m (xi, xj) представляет собой стоимость строительства дороги, напрямую связывающей города xi и xj, то решение задачи о минимальном каркасе для этого графа показывает, как связать эти города дорогами так, чтобы из любого города можно было попасть в любой другой при минимальных затратах на строительство.
Алгоритм решения задачи:
1) выбрать в графе ребро, имеющее минимальную меру (если таких ребер несколько, взять любое из них);
2) выбрать из оставшихся ребер ребро, имеющее минимальную меру, так, чтобы добавление этого ребра не приводило к образованию цикла (если при добавлении такого ребра образуется цикл, то берется следующее минимальное по мере ребро);
3) повторять шаг 2 до тех пор, пока не будет построен каркас графа.
Из свойств деревьев следует, что построение завершается за n - 1 шаг, где n – количество вершин графа.
2.5.3. Поиск кратчайших и длиннейших путей в графе
Алгоритм Форда.
Существуют два варианта этого алгоритма, один из которых используется для поиска кратчайшего пути, а другой – длиннейшего пути между двумя заданными вершинами.
В обоих случаях процесс поиска состоит из трех этапов. На первом этапе производится присвоение вершинам графа некоторых индексов (индекс, присваиваемый вершине хi, будем в дальнейшем обозначать li). На втором этапе, который состоит из нескольких шагов, эти индексы изменяются по определенным правилам, пока выполняется некоторое условие. В конце второго этапа значения индексов стабилизируются. На третьем этапе строится искомый путь.
Рассмотрим эту процедуру сначала для поиска кратчайшего пути в графе с нагруженными ребрами. Обозначим начальную вершину х0, а конечную хn.
1-й этап. Вершине х0 присваивается индекс l0 =0, а остальным вершинам хi
(i ¹ 0) присваиваются индексы li = ¥.
2-й этап. Ищется дуга (хi, хj), для которой разность между конечным и начальным индексом больше меры этой дуги:
lj - li > m (хi, хj) (2.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.