Пример 2.10. В графе G = (X, Г), заданном матрицей смежности M(G), найти все максимальные сильно связные подграфы. Для сокращения записи у строк и столбцов матрицы проставим не полные обозначения вершин, а только их номера.
1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 0 1 0 0 0
1
0 1 1 0 0 0 0 0 0 0 2
0 0 1 0 0 0 0 0 1 0 3
0 0 1 1 0 0 0 0 0 0 4
M(G) = 0 0 0 0 0 0 0 0 0 1 5
0 0 0 0 1 1 0 0 0 0 6
0 0 0 0 0 0 0 1 0 0 7
1 0 0 0 0 0 0 0 1 0 8
0 1 0 0 0 0 1 0 0 1 9
0 0 0 0 0 1 0 0 0 0 10
Является ли этот граф сильно связным?
Решение. Воспользуемся для решения задачи алгоритмом Мальгранжа.
Выберем
произвольную вершину, например, х1, и, используя M(G), найдем множества
достижимости и обратной достижимости этой вершины 
.
Элементы первого множества выделим цифрами в дополнительном столбце справа от
матрицы смежности, а элементы второго множества – в дополнительной строке под
матрицей. Эти цифры означают расстояние от х1 до вершины xi
(i = 2, 3, ...,10) в первом случае и расстояние от xi до х1
во втором. Вершины, не достижимые из х1 в графе G (или G-1), отметим крестиками в
дополнительном столбце (или в дополнительной строке).
1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 0 1 0 0 0 1 0 
0 1 1 0 0 0 0 0 0 0 2 4
0 0 1 0 0 0 0 0 1 0 3 5
0 0 1 1 0 0 0 0 0 0 4 х
M(G) = 0 0 0 0 0 0 0 0 0 1 5 6
0 0 0 0 1 1 0 0 0 0 6 5
0 0 0 0 0 0 0 1 0 0 7 1
1 0 0 0 0 0 0 0 1 0 8 2
0 1 0 0 0 0 1 0 0 1 9 3
0 0 0 0 0 1 0 0 0 0 10 4
0
5 4 4 х х 2 1 3 х 
 |
Выпишем в явном виде множество вершин, достижимых из вершины х1
и множество обратной достижимости этой вершины:
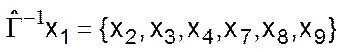
Множество вершин максимального сильно связного подграфа, содержащего вершину х1,
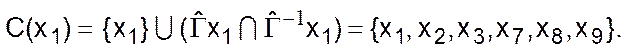
Так как это множество включает в себя не все вершины графа G, то граф G не является сильно связным.
Матрица смежности полученного подграфа получается из элементов исходной матрицы, стоящих на пересечении столбцов с номерами 1, 2, 3, 7, 8, 9 и строк с теми же номерами:
1 2 3 7 8 9
0 0 0 1 0 0 1
0 1 1 0 0 0 2
M[C(x1)] = 0 0 1 0 0 1 3
0 0 0 0 1 0 7
1 0 0 0 0 1 8
0 1 0 1 0 0 9
Постройте с помощью этой матрицы соответствующий подграф и убедитесь, что он является сильно связным, т.е. в нем из любой вершины можно попасть в любую другую по некоторому пути.
Вычеркнем из матрицы M(G) строки и столбцы, соответствующие элементам множества C(х1). В результате получим матрицу М1 подграфа графа G, определенного на всех вершинах исходного графа, не вошедших в C(х1):
4 5 6 10
1 0 0 0 4
М1 = 0 0 0 1 5
0 1 1 0 6
0 0 1 0 10
В полученном подграфе выберем произвольную вершину, например, х4, и произведем операции, аналогичные описанным выше.
4
5 6 10
1 0 0 0 4 0
М1 = 0 0 0 1 5 х
0 1 1 0 6 х
0 0 1 0 10 х
 |
0 х х х
|
В результате имеем С(х4)= {х4}, т.е. этот максимальный сильно связный подграф содержит всего одну вершину х4 с петлей в этой вершине. Его матрица смежности содержит всего один элемент
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.